드디어 행렬의 특성들과 특별한 행렬들에 대해서 정리한다.
이번 장에서는 다음 내용들을 배운다.
- Linear Combination (선형 결합)과 Span
- Linearly Independent (선형 독립)과 Basis (기저)
- 항등 행렬
- 역 행렬
- 역 행렬의 존재 조건
- 기타 특별한 행렬과 벡터
- Diagonal Matrix (대각 행렬)
- Symmetric Matrix (대칭 행렬)
- Unit Vector (단위 벡터)
- Orthogonal Matrix (직교 행렬)
- Rank
- Null Space
Linear Combination과 Span

이전 장에서 Vector들의 Row Space, Column Space에 대해서 약간 맛보기를 해 보았다.
Vector들은 서로 더하고 빼며 Space를 이루게 되는데 이렇게 만들어진 Space를 Span이라 부른다.
다시 정확히 표현하자면, Span이란 주어진 벡터들의 linear combination으로 이루어진 Space를 의미한다 볼 수 있다.
그렇다면 Linear Combination이란 무엇인가?
Linear Combination
Linear Combination(선형 결합)이란 벡터와 스칼라의 연산을 통해 새로운 벡터를 생성하는 방법을 의미하며 이때 연산은 벡터의 선형적인 연산인 덧셈과 뺄셈과 스칼라 곱만이 가능하다.
즉, 수식으로 나타내면 다음과 같다.
$$
a_1v_1 + a_2v_2 + ... + a_nv_n
$$
이때 각 $a_i$는 스칼라이다.
좀 더 상세히 예를 들어 2차원 벡터 $v_1 = \begin{bmatrix}
1 \\
2
\end{bmatrix},
v_2 = \begin{bmatrix}
3 \\
4
\end{bmatrix}$가 있을 때 이 두 벡터로 만들어지는 선형 결합은 다음과 같이 표현할 수 있다.
$$
a_1v_1 + a_2v_2 = \begin{bmatrix}
a_1 + 3a_2 \\
2a_1 + 4a_2
\end{bmatrix}
$$
이때 $a_1, a_2$는 어떤 스칼라 값이든 될 수 있다.
즉, Span이란 특정 벡터 집합 내의 벡터들을 스칼라 배하여 더하고 빼 만들어지는 공간을 의미한다.
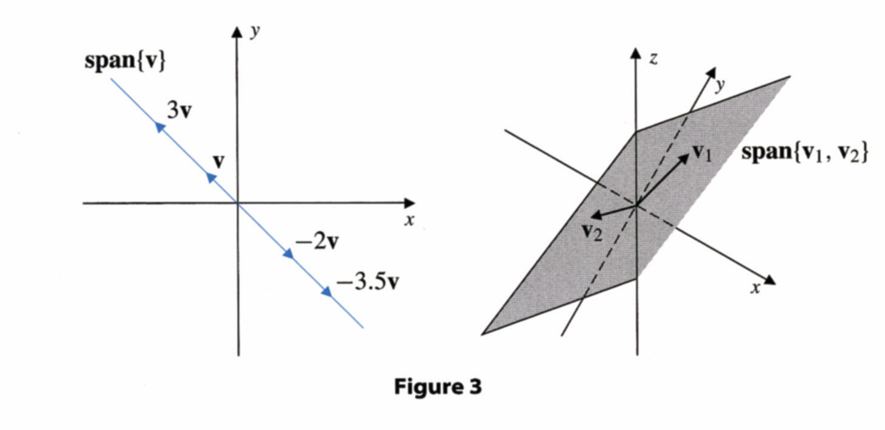
위 그림을 보면 더 이해가 되는데, 벡터 $\textbf v$ 하나의 span의 경우 직선 하나가 되지만, 두 벡터 $\textbf v_1, \textbf v_2$의 span의 경우 평면을 이루게 된다. (이렇게 평면을 이루지 않고 직선을 이룰 수도 있음 아래 파트에서 더 자세히..)
글로만 이해가 안 가는 경우 아래 영상이 여러가지 벡터의 linear combination을 영상화 해 보여주어 이해에 큰 도움이 된다.
https://www.youtube.com/watch?v=g0eaDeVRdZk&list=PL_iJu012NOxdZDxoGsYidMf2_bERIQaP0&index=8
Linearly Independent와 Basis
이때 재미있는 점으로 벡터들의 Linear Combination으로 나타낼 수 있는 Span의 차원이 벡터 집합마다 차이가 있다는 점이다.

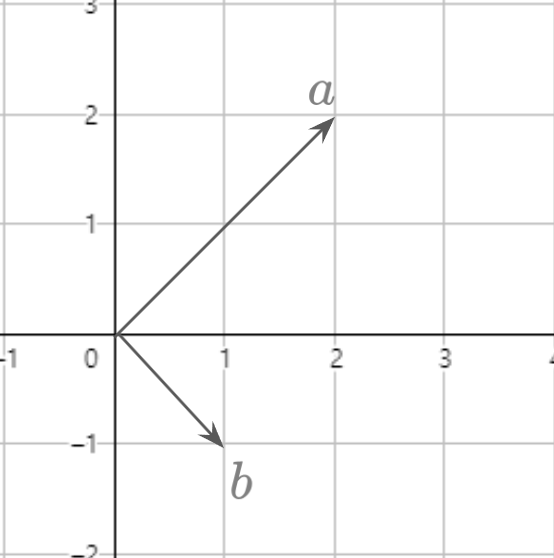
예를 들어 오른쪽 그림과 같이 $\textbf a$와 $\textbf b$가 있는 경우 이 둘의 Linear Combination으로 2차원 좌표 평면을 모두 채울 수 있다. 하지만 왼쪽 그림과 같이 $\textbf a$와 $\textbf c$는 한 직선 위에 존재하기 때문에 $y = x$ 직선만을 만들어낼 수 있을 뿐이다.
이것과 관련된 것이 바로 벡터들의 Linearly Independent (선형 독립)의 여부이다.
그렇다면 선형 독립이란 무엇일까? 선형이란 말은 이제 익숙하니 알겠는데 “독립”이라는 말이 아직은 낯설다. 여기서 얘기하는 독립이란, 특정 벡터 집합에서 벡터들 사이의 관계를 의미한다.
만약 벡터 집합 $K = {v_1, v_2, v_3, v_4}$가 있다고 해보자. 이때 $v_1, v_2, v_3$의 linear combination이 $v_4$와 동일한 벡터를 만들어 낼 수 있다면 이 벡터 집합은 선형 독립이 아니다. 이렇게 선형 독립이 아닌 것을 선형 종속 (linearly dependent)라 부른다.
다른 블로그들을 보면 선형 독립을 $a_1v_1 + a_2v_2 + a_3v_3 + a_4v_4 = 0$와 같이 표현하는 경우도 존재하는데 여기서 $a_4v_4$를 오른쪽으로 이항하면 위에서 얘기한 것과 동일하다.
아무튼 결과적으로 위 벡터 집합 $K$에서 $v_4$가 빠져도 $K$의 Span에는 아무 영향이 없다는 것이다.
다시 위 예시 그림을 보면 $a$로는 아무리 늘리고 줄여도 $b$를 만들어내지 못하지만, $c$에 -2 스칼라 배를 해주면, $a$를 만들어낼 수 있다. 즉, 왼쪽 그림은 서로 독립인 두 벡터를 보여주며, 오른쪽 그림은 서로 독립이 아닌. 즉, 서로 종속인 두 벡터 $a, c$를 보여주는 그림이다.
결과적으로 오른쪽 두 벡터는 선형 결합으로 2차원을 span하며, 오른쪽 두 벡터는 하나가 빠져도 상관이 없으므로 1차원을 span할 수 밖에 없다.

물론 위와 같이 3 개가 있는 경우도 선형 종속(linearly dependent)이다. 이 경우 a, b, d 중 아무거나 하나가 빠져도 span의 결과가 2 차원이므로 선형 종속이라 볼 수 있다.
이때 당연하지만 생각하기 어려운 점이 있는데 $0$ 벡터가 존재하는 경우 다른 모든 벡터에 스칼라 0배를 해주면 되기 때문에 선형 종속이 된다는 것이다.
Basis
Basis는 linearly indenpendent와는 반대로 특정 차원을 span하는 서로 linearly independent를 미리 가정한 벡터들을 의미한다.
예를 들어 2차원의 basis는 ${\begin{bmatrix}
1 \\
0
\end{bmatrix}, \begin{bmatrix}
0 \\
1
\end{bmatrix}}$, ${\begin{bmatrix}
3 \\
1
\end{bmatrix}, \begin{bmatrix}
1 \\
1
\end{bmatrix}}$ 등 굉장히 많다. 서로 선형 독립이기만 하면 되는 n차원 벡터 n개를 Basis(기저)라 부른다.
정리하면 다음과 같다.
- Basis - 이미 선형 독립을 가정한 특정 차원을 span할 수 있는 벡터들
- linearly indenpendent - 특정 벡터들의 선형 결합이 영 벡터를 만들 수 없는 벡터들인 경우 또는 임의의 한 벡터를 다른 벡터들의 선형 결합으로 만들 수 없는 경우를 의미.
항등 행렬
혹시 항등원이라는 것에 대해 안다면 항등 행렬이 뭔지 감이 올 것이다. 모른다면 어쩔 수 없이 아래 토글을 열어야 하겠지..?
항등원이란?
- 예를 들어 덧셈의 항등원은 0, 곱셈의 항등원은 1이다.
- 간단히 얘기하면 임의의 수 $\alpha$와 어떤 수 $\epsilon$를 특정 연산 $f$를 취했을 때 그 결과가 $\alpha$로 동일하게 나온다면 특정 연산 $f$의 항등원을 $\epsilon$이라 부른다. $f(\alpha, \epsilon) = \alpha$
항등 행렬이란 행렬의 곱셈의 항등원을 의미한다. 즉, 임의의 행렬 $A$와 항등 행렬 $I$를 곱한 결과는 $A$로 항상 동일하다는 것이다. $(AI = IA = A)$
$$
I = \begin{bmatrix}
1 & 0 & ... & 0 \\
0 & 1 & ... & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & ... & 1
\end{bmatrix}
$$
일반적으로 항등행렬은 $I$로 표기하며 위와 같이 주 대각 요소가 모두 1이고 다른 요소들은 0인 정사각 행렬들이 항등 행렬이다.
실제로 행렬을 보면 그냥 왼쪽에서 곱했을 경우 $(IA)$ i 번째 row 벡터는 i 번째 row vector을 잡아내어 결과 행렬의 i 번째 row vector에 넣어주는 역할을 하며, 오른쪽에서 곱했을 경우$(AI)$ i 번째 column 벡터는 i번째 요소만 1이므로 $A$의 i번째 column 벡터를 결과 행렬의 i번째 column 벡터에 넣어주어 그대로 나오게 한다.
역 행렬
역 행렬도 역원이라는 것을 안다면 감이 올 것이다. 역시 모른다면 아래 토글을 열어 읽어 봐야겠지..?
역원이란?
- 실수 덧셈에서는 $-x$가 역원이며, 0을 제외한 곱셈의 역원은 $\frac{1}{x}$가 된다.
- 간단히 말해 두 수 $a, b$를 연산 $f$를 한 결과가 항등원일 때 b를 $a$의 역원, $a$를 $b$의 연산 f에 대해 역원이라 부른다. $f(a, b) = \epsilon, f(a, \epsilon) = a$
역 행렬이란 특정 정 사각 행렬 $A$에 곱했을 때 항등 행렬이 나오게 해주는 정 사각 행렬을 의미하며 $A^{-1}$로 표기한다.
이러한 역 행렬을 알고 있다면 $Ax = b$라는 방정식을 쉽게 풀어낼 수 있을 것이다. (양 변 왼쪽에 $A^{-1}$을 곱하면 $x=A^{-1}b$가 바로 나온다.)
이러한 역행렬을 구하는 방법에 대해서는 다음 장에서 자세히 살펴보도록 하자.
기타 특별한 행렬과 벡터들
Diagonal Matrix (대각 행렬)
$$
D = \begin{bmatrix}
d_1 & 0 & ... & 0 \\
0 & d_2 & ... & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & ... & d_n \\
\end{bmatrix}
$$
대각 행렬은 위와 같이 주 대각선 요소를 제외한 모든 요소가 0인 행렬을 의미하며 앞서 배운 항등 행렬 또한 이 대각 행렬에 속하게 된다.
이러한 대각 행렬은 주 대각선 요소만이 다르기 때문에 $diag(v)$로 벡터 $v$의 요소가 주 대각선 요소인 대각 행렬을 표현한다.
대각 행렬은 매우 계산이 편리한 특성을 지니는데, 다음과 같다.
- 행렬의 거듭 제곱이 각 요소의 거듭 제곱만 해주면 되기 때문에 매우 간단해짐
- 대각 행렬과 벡터의 곱의 경우 단순히 벡터의 성분마다 곱셈을 하는 것으로 매우 간단해짐. 이는 column vector의 모음인 행렬의 곱셈에도 적용 가능
- determinant가 대각 요소의 곱으로 표현됨 (즉, 대각 요소에 0이 없는 경우 역행렬이 존재)
- 역 행렬이 대각 요소를 역수를 취한 대각 행렬이다.
이러한 계산적 이점 덕에 앞으로도 계속 나오게 된다.
Symmetric Matrix (대칭 행렬)
$$
\begin{bmatrix}
1 & 2 & 3 \\
2 & 4 & 5 \\
3 & 5 & 6
\end{bmatrix}^T = \begin{bmatrix}
1 & 2 & 3 \\
2 & 4 & 5 \\
3 & 5 & 6
\end{bmatrix}
$$
대칭 행렬은 위와 같이 Transpose를 해도 기존 행렬과 동일한 행렬을 의미한다. $(A = A^T)$ 이러한 특성에서 알 수 있듯이 당연하게도 대칭 행렬은 정 사각 행렬에서만 정의된다.
이는 모든 i,j에 대해서 $a_{ij} = a_{ji}$가 성립한다는 것을 의미하며, 앞으로 나올 고유갑 분해 등에서 이 행렬의 특별한 특성들이 소개된다.
또 대칭 행렬의 제곱도 대칭 행렬이라는 간단히 확인해 볼 수 있는 특성도 존재한다.
Unit Vector (단위 벡터)
단위 벡터는 방향에 상관 없이 단순히 크기가 1인 벡터를 의미한다.
이런 벡터들은 단순히 특정 방향을 나타내고 싶을 때 자주 사용하게 된다.
💡 예를 들어 벡터 $\textbf a$와 $\textbf b$가 존재할 때 $\textbf a$를 $\textbf b$에 정사영 내린 벡터를 나타낼 경우 $\textbf b$ 방향의 unit vector와 $\textbf a$를 내적 후 그 크기를 $\textbf b$ 방향의 unit vector와 곱해주면 얻을 수 있다.
Orthogonal Matrix (직교 행렬)
직교 행렬이란 모든 Column 벡터가 서로 직교하는 정 사각 행렬을 의미한다.
이 행렬을 Transpose하게 되면 역행렬이 되는 매우 중요한 특성이 존재한다.
즉, $QQ^T = Q^TQ = I$가 성립하는 $Q$는 직교 행렬이다. 이때 $Q$의 각 column 벡터들은 noramlize 되어 있어야만 한다. (아니면 $I$가 안 나옴. 각 column 벡터는 서로 수직하기 때문에 $a_{i i}$ 요소만이 0이 아닌 요소가 나오게 되는 것은 당연하다 볼 수 있다.)
이렇게 normalize 된 orthogonal column 벡터들을 orthonormal(정규 직교)이라 부른다.
Rank
Rank란 행렬이 가지는 independent한 Column vector의 개수를 의미하며 이는 곧 Column Space의 dimension을 의미하게 된다.
또 다르게 표현하면 Column Vector의 Span의 차원을 의미한다 할 수 있다.
또 아래와 같은 매우 중요한 특성이 있다.
Independent 한 Column의 수 = Independent한 Row의 수. 즉, $rank(A) = rank(A^T)$
위 특성은 즉, row space의 dimension = column space의 dimension과 같다는 의미이다.
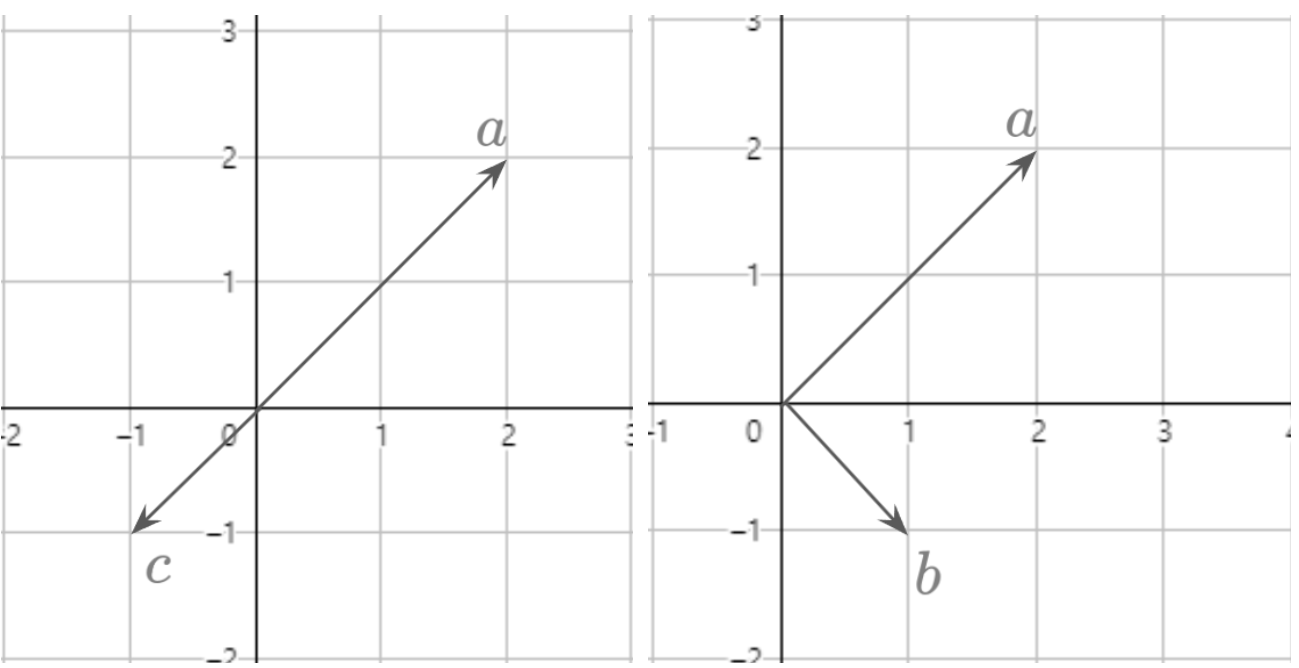
다시 위 예시를 가져와서 보자. 오른쪽 그림은 서로 independent(독립)하기에 xy 평면을 span하며 Rank는 2이다. 반대로 왼쪽 그림은 서로 dependent(종속)하기에 $y = x$를 span하므로 Rank는 1이다.
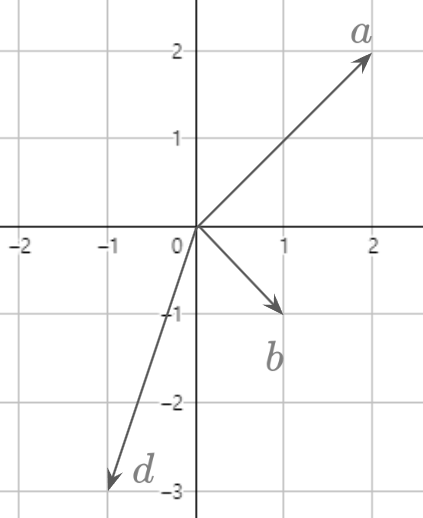
마지막으로 위 그림은 $-a+b = d$이므로 선형 종속이며, 이 벡터 집합은 2차원을 span하므로 Rank는 2이다.
$$
\begin{bmatrix}
2 & 1 & -1 \\
2 & -1 & -3
\end{bmatrix}
$$
이를 행렬로 표현하면 위와 같다. 이때 서로 독립인 column 벡터는 2개이며, 서로 독립인 row vector도 2개이다. 이로써 앞서 말한 row rank = column rank임을 알 수 있다.
위 행렬은 $2\times 3$ 행렬이므로 row 벡터에서 최대 가질 수 있는 rank는 2이다. 이때 row rank는 2로 최대 가질 수 있는 갯수 만큼 가지고 있으므로 이는 full row rank라 부른다.
$$
\begin{bmatrix}
2 & 1 & -1 \\
0 & 0 & 0
\end{bmatrix}
$$
반대로 위와 같은 행렬에서 row rank는 최대 2개인데, rank는 1이므로 이러한 경우를 row rank deficient라 부른다.
반대로 column의 경우에도 column에서 최대 가질 수 있는 rank를 모두 가졌다면, full column rank, 가지지 못했다면 column rank deficient라 부른다.
정 사각 행렬의 경우에는 row의 개수 = column의 개수이므로 그냥 full rank, rank deficient라 부른다.
Null Space
Null Space는 지금까지 본 Column Space, Row Space와 같이 어떤 Space를 의미한다.
이때 Null이란 영어로 “존재하지 않는”다는 뜻을 가지고 있다.
선형대수학에서 Null Space란 $Ax = 0$을 만족하는 $x$의 집합을 의미한다.
$$
A = \begin{bmatrix}
0 & 1 & 1 \\
1 & 0 & 1
\end{bmatrix}
Ax = x_1\begin{bmatrix}
0 \\
1
\end{bmatrix} + x_2\begin{bmatrix}
1 \\
0
\end{bmatrix} + x_3\begin{bmatrix}
1 \\
1
\end{bmatrix} = \begin{bmatrix}
0 \\
0
\end{bmatrix}
$$
예를 들어 위와 같이 있을 때 매우 trivial 한 solution은 $x = 0$이다.
또 다른 Solution은 $\begin{bmatrix}
1 \\
1 \\
-1
\end{bmatrix},\begin{bmatrix}
2 \\
2 \\
-2
\end{bmatrix}$ 등이 존재하며, 이는 $c\begin{bmatrix}
1 \\
1 \\
-1
\end{bmatrix}$로 표현할 수 있다. 즉 위 예시에서 Null Space의 차원은 1 차원 직선이 표현하게 된다.
A의 shape가 $m \times n$일 때 $\dim(N(A)) = n - r$로 표현할 수 있다. ($r$은 row vector의 span)
💡 이는 **row vector가 존재하는 차원에서 row vector의 span의 차원을 뺀 것**으로 즉, **row vector들과 수직인 녀석들로 만들어내는 공간이 Null Space**라는 것으로 해석이 가능하다.
지금까지 본 것은 Right Null Space로 일반적으로 Null Space라 불리는 녀석이다.
당연하게도 Left Null Space $N_L$도 있는데, $x^TA = 0$인 $x$가 만들어 내는 집합으로 여기서 Null Space는 Column Space와 수직한다.
Rank에 따른 $Ax = b$의 해의 개수
그렇다면 행렬 $A$의 rank에 따른 선형 방정식 $Ax=b$의 해의 개수에 대해서 알아보자.
먼저 행렬 $A$의 rank는 위에서 언급한 대로 full column rank, full row rank, full rank, rank deficient가 될 수 있다.
- Full Column Rank인 경우
- 해가 유일하다.
- 만약 $b$가 A의 Column Space 안에 들어온다면 유일하게 $x$가 결정되기 때문에 해가 유일하게 존재하게 된다.
- 해가 존재하지 않는다.
- 만약 $b$가 A의 Column Space안에 들어오지 않게 되면 A의 Column Vector들의 선형 결합으로 $b$를 만들 수 없기 때문에 해가 존재하지 않는다.
- 이 경우 행렬 A는 세로로 길쭉한 행렬이 되며, b는 A의 Column vector와 차원이 같아진다.
- Full Row Rank인 경우이때 Row Space의 Null Space에 존재하는 벡터들을 그냥 정답 $x$에 더해도 0벡터 + $b$의 결과가 나와 이 결과도 $b$가 되므로 해가 무한해진다.
- 이 경우 행렬 A는 가로로 길쭉한 행렬이 되며, row vector의 rank는 column vector의 차원이 될 것이다. 즉, 항상 $b$를 표현할 수 있게 된다.
- Full Rank인 경우
- 행렬 $A$의 Column Space가 Column vector들이 존재하는 차원과 동일하므로 해는 언제나 유일하다.
- Rank Deficient인 경우
- 해가 없다.
- 이 경우는 행렬 A의 랭크가 행렬의 최대 가능 rank보다 작으므로 행렬 $A$의 Column Space는 A의 Column Vector들이 존재하는 차원 전체를 Span하지 못하므로 $b$가 Column Space에 존재하지 않는 경우 해가 없다.
- 무한히 많은 해가 있다.
- $b$가 만약 $A$의 Column Space에 속한다면, 특정한 해 벡터 $x$를 하나 계산할 수 있을 것이다. 여기에 A의 null space에 속하는 벡터들을 더해도 동일한 $b$를 얻을 수 있으므로 무한히 많은 해를 가진다.
이번 장에서는 여러가지 역행렬, 항등 행렬과 같은 특별한 행렬 몇 가지와 Span, 선형 독립, 종속. 선형 결합, Rank와 같은 여러가지 행렬의 특성들에 대해서 살펴보았다.
Reference
'공부 및 정리 > 선형대수학' 카테고리의 다른 글
| 최소 자승법 (0) | 2023.10.02 |
|---|---|
| 가우스-조던 소거법과 역행렬 (0) | 2023.09.29 |
| 행렬과 벡터의 기초 연산 (0) | 2023.09.25 |
| 행렬과 벡터의 기초 (0) | 2023.09.25 |
| 선형대수학 개요 (0) | 2023.09.25 |



