가우스-조던 소거법과 역행렬
이번 장에서는 가우스-조던 소거법이라는 연립 일차 방정식을 풀어내는 알고리즘과 이전 장에서 배운 역행렬에 관해 더 깊게 알아본다.
이번 장에서는 이러한 내용을 다룬다.
- 가우스-조던 소거법
- 역 행렬
- 행렬식 (Determinant)
- 행렬식의 기하학적 의미
- 행렬식 (Determinant)
가우스-조던 소거법

가우스-조던 소거법은 그냥 단순히 연립 일차 방정식을 풀어내는 알고리즘으로 그냥 우리가 중고등학교에서 연립 방정식을 풀어내는 것을 일반화한 것에 불과한 알고리즘이다.
$$
\begin{matrix}
4x_1 + 2x_2 = 18 \\
x_1 - x_2 = 3
\end{matrix}
$$
위와 같은 미지수가 2개인 연립 방정식이 존재한다고 하자. 이때 우리는 본능적으로 아래 식에 2를 곱해 위 식에 더해 $x_1$을 구해버릴 것이다.
하지만 이 방식은 미지수와 연립 식이 매우 많아지면 귀찮아진다. 이를 실수하지 않게 알고리즘으로 정립한 것이 바로 가우스 조던 소거법인 것이다.
위 식을 그냥 행렬식으로 다음과 같이 단순히 표현할 수 있다.
$$
\begin{bmatrix}
4 & 2 \\
1 & -1
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2
\end{bmatrix}=
\begin{bmatrix}
18 \\
3
\end{bmatrix}
$$
이것도 귀찮아서 보통 아래와 같이 상수들만 한번에 표현하며 이를 Augmented Matrix(확장 행렬)라 부르는데 딱히 용어는 중요하지 않다. 그냥 이렇게 표현한다는 것을 알면 된다.
$$
\begin{bmatrix}
4 & 2 & | & 18 \\
1 & -1 & | & 3
\end{bmatrix}
$$
위와 같이 표현하면 | 기준으로 왼쪽을 Coefficient Matrix라 부르며 이 부분에 가우스 조던 소거법 알고리즘을 적용한다.
2가지 규칙을 사용하는 것이 가우스-조던 소거법이다.
- 임의의 row vector에 상수 배하여 다른 임의의 row vector에 더해 주 대각선 아래 요소들을 0으로 만들어 상 삼각 행렬을 만든다. 이때 row vector 결과에 그대로 상수 배하여 빼줘도 된다.
- 주 대각선 위 요소들을 0으로 만든다.
이때 상 삼각 행렬이란 그냥 단순히 주 대각선 아래 요소가 전부 0인 경우이면 상 삼각 행렬이라 부른다. 반대로 주 대각선 아래 요소들이 전부 0이면 하 삼각 행렬이라 부른다.
이 과정을 거치면 주 대각선 요소만이 남으며, 이 요소들을 1로 만들면 | 우측 요소들이 바로 우리가 찾던 값이 된다.
이때 행의 위치를 교환해도 된다는 점을 유념하자. 이는 단순히 연립 방정식의 방정식 순서를 바꾸는 것으로 결과에 영향을 주지는 않는다.
위 예시에 적용해보면 먼저 2 행을 1 행과 교환해 1행 1열의 값을 1로 만들어주자.
$$
\begin{bmatrix}
1 & -1 & | & 3 \\
4 & 2 & | & 18
\end{bmatrix}
$$
1 행에 4 스칼라 배를 한 후 2 행에 빼 주 대각선 하단 부를 0으로 만든다.
$$
\begin{bmatrix}
1 & -1 & | & 3 \\
0 & 6 & | & 6
\end{bmatrix}
$$
이후 2행에 $\frac{1}{6}$을 곱해 1행에 더해주면 주 대각선 요소만 남고 주 대각선 요소를 1로 만들어주면 다음과 같다.
$$
\begin{bmatrix}
1 & 0 & | & 4 \\
0 & 6 & | & 6
\end{bmatrix} \rightarrow \begin{bmatrix}
1 & 0 & | & 4 \\
0 & 1 & | & 1
\end{bmatrix}
$$
즉, $x_1 = 4, x_2 = 1$이 된다.
역 행렬
이전에도 배운 것처럼 특정한 정 사각 행렬 $A$의 역 행렬 $A^{-1}$이란 $A$와 곱했을 때 항등 행렬 $I$가 결과로 나오는 행렬로 대충 뭔 느낌인지 정도만 알고 넘어갔다.
하지만 이젠 제대로 배워야 할 때!
$$
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}^{-1} =
\frac{1}{ad - bc}
\begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix}
$$
역 행렬은 우리가 고등학교 1학년 시절의 기억을 떠올려 보면 $2 \times 2$ 행렬에서 아래와 같이 정의 되었다.
근데 생각해보면 그냥 이게 이런 공식이야~ 하고 배우고 어떻게 나온 것인지는 기억이 나질 않는다. 이게 어떻게 얻어지는지 먼저 알아보도록 하자.
$AA^{-1} = I$라는 공식에서 시작해 $A^{-1} = \begin{bmatrix}
x_1 & x_2 \\
x_3 & x_4
\end{bmatrix}$로 표현하면 다음과 같다.
$$
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} \begin{bmatrix}
x_1 & x_2 \\
x_3 & x_4
\end{bmatrix} =
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
$$
이는 이전에 배운 가우스 조던 소거법으로 구할 수 있다.
$$
\begin{bmatrix}
a & b & | & 1 & 0 \\
c & d & | & 0 & 1
\end{bmatrix}
$$
이전처럼 Augmented Matrix 꼴로 만들어 주어 왼쪽 부분을 항등 행렬로 만들어주면 우측 부분이 우리가 찾던 $A^{-1}$이 될 것이다.
$$
\begin{bmatrix}
a & b & | & 1 & 0 \\
c & d & | & 0 & 1
\end{bmatrix} \rightarrow \begin{bmatrix}
a & b & | & 1 & 0 \\
0 & d - \frac{bc}{a} & | & -\frac{c}{a} & 1
\end{bmatrix} \\
\rightarrow
\begin{bmatrix}
a & 0 & | & 1 + \frac{bc}{ad - bc} & -\frac{ab}{ad-bc} \\
0 & d - \frac{bc}{a} & | & -\frac{c}{a} & 1
\end{bmatrix} \\
\rightarrow
\begin{bmatrix}
1 & 0 & | & \frac{d}{ad - bc} & -\frac{b}{ad-bc} \\
0 & 1 & | & -\frac{c}{ad-bc} & \frac{a}{ad-bc}
\end{bmatrix} \\
\therefore A^{-1} = \begin{bmatrix}
\frac{d}{ad - bc} & -\frac{b}{ad-bc} \\
-\frac{c}{ad-bc} & \frac{a}{ad-bc}
\end{bmatrix} =
\frac{1}{ad-bc} \begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix}
$$
최종 결과가 고등학교 때 배운 공식과 동일한 것을 확인 가능하다.
이때 $ad-bc \neq 0$ 이어야만 $A^{-1}$이 존재한다는 것을 알 수 있고 이를 Determinant(행식)라 부른다.
이러한 $A^{-1}$이 존재한다는 것을 Invertible 하다라고 표현하며, 이를 아래와 같이 달리 표현하기도 한다.
- $\det(A) \neq 0$
- $A$가 Full Rank이다. ⇒ $\det(A) = 0 \leftrightarrow A$가 Rank Deficient이다.
- $N(A) = 0$. 즉, Null Space가 0 벡터밖에 없다는 것으로 column 벡터들이 전부 independent라는 것이다.
이러한 역행렬 관련 Property는 다음과 같다.
- $(AB)^{-1} = B^{-1}A^{-1}$
- 이를 다시 $AB$와 곱해보면 $AB(AB)^{-1} = ABB^{-1}A^{-1} = AIA^{-1} = I$
- $(A^{-1})^{-1} = A$
- $(kA)^{-1}=\frac{1}{k}A^{-1}$
- $(A^T)^{-1} = (A^{-1})^T$
- $\det(A^{-1}) = \frac{1}{\det(A)}$
행렬식(Determinant)
위에서 언급한 행렬식에 대해서 조금만 더 자세히 살펴보자.
먼저 Determinant 관련 property에 대해서 알아보자.
- $\det(A) = 0 \leftrightarrow A$는 not invertible (Singular Matrix)
- A가 rank deficient $\leftrightarrow \det(A) = 0$
- 대각 행렬에 대해서는 대각 성분의 곱으로 행렬식을 구할 수 있다. 즉, $\det(A) = \sum_i A_{i,i}$
- 삼각 행렬의 Determinant에 대해서도 대각 행렬과 동일하다.
- 항등 행렬의 Determinant는 1이다. (3번에서 나오는 결과)
- $\det(cA) = c\det(A)$
- $\det(A^T) = \det(A)$
- $\det(AB) = \det(A)\det(B)$
- 이 공식은 매우 자주 나오므로 꼭 기억해 두자.
- $\det(A^{-1}) = \frac{1}{\det(A)}$
- $\det(A) = \sum \lambda_i$여기서의 $\lambda$란 $A$의 고유값으로 $A$로 인한 선형 변환 시 특정 방향으로 얼마만큼의 변화를 주는 지에 대해서 나타내는 값이라고 만 알아두면 훌륭하다.
- 이는 아까 본 Determinant가 행렬의 선형 변환에서 공간을 어떻게 확장하거나 압축하는지에 대한 내용과 일치하는 것을 알 수 있다.
- 갑자기 $\lambda$라는 기호가 나와서 당황스럽지만 이것은 다다음 장에서 배울 고유 값 분해와 관련된 내용이다. 일단은 필요할 것 같아서 넣어둔다.
- 행렬 내 한 행 또는 열에 스칼라 배 시 determinant도 그 스칼라가 곱해짐
- 행렬 내 한 행이나 열이 다른 행이나 열에 더해질 경우 determinant는 변하지 않음
- (즉, determinant를 편하게 구하기 위해 삼각 행렬로 만들 수 있다는 의미)
아래 내용은 어려우면 그냥 넘어가도 좋을듯?
행렬식의 기하학적 의미
행렬식은 앞에서 언급한 것처럼 이 정 사각 행렬이 Invertible 한지 아닌지 판별에 자주 사용된다. 하지만 이것 외에도 행렬의 선형 변환 특성에 대한 정보들을 포함한다.
- 확장 및 압축에 대한 정보

예를 들어 항등 행렬 $I$에 대해 생각해보자. 이 항등 행렬과 곱을 할 시 항상 그대로 나온다는 것은 이미 우리에게 익숙하다. 즉, 항등 행렬은 선형 변환 후 공간의 부피를 유지 시킨다는 것이므로 Determinant는 1이어야만 하는데 실제로 계산해보면 $ad-bd = 1-0 = 1$이 나오게 된다.
항등 행렬이 아닌 다른 경우에 대해서도 살펴보자. 일반적으로 행렬식의 기하학적 특성은 여러개의 벡터가 이루는 공간의 부피를 변화시키는 것을 말한다.
아래와 같이 행렬식의 기하학적 특성에 대해 행렬식이 3이고, 임의로 선택한 두 벡터를 예시로 간단히 살펴보도록 하자.
$$
A = \begin{bmatrix}
1 & -1 \\
1 & 2
\end{bmatrix},
\textbf{v}_1 = \begin{bmatrix}
1 \\
0
\end{bmatrix},
\textbf{v}_2 = \begin{bmatrix}
1 \\
2
\end{bmatrix}
$$

$\textbf{v}_1, \textbf{v}_2$가 이루는 평행사변형의 넓이는 위 그림과 같이 $2 \times 1 = 2$다.
이를 A와 곱한 결과는 아래와 같다.
$$
A\textbf{v}_1 = \begin{bmatrix}
1 \\
1
\end{bmatrix},
A\textbf{v}_2 = \begin{bmatrix}
-1 \\
5
\end{bmatrix}
$$

이 영역의 넓이는 [-1, 1]을 밑 변으로 하고, [0, 6]을 높이로 하는 직사각형에서 양쪽 삼각형들을 빼주면 넓이를 얻을 수 있다.
직사각형의 넓이는 $2 \times 6 = 12$, 양쪽 삼각형의 총 넓이는 $(1\times 1 \times + 1 \times 5) \times \frac{1}{2}\times 2 = 6$으로 최종 넓이는 $12 - 6 = 6$이 된다.
이전 넓이 2에서 6으로 변했으므로 행렬식 3만큼 넓이가 변화한 것을 확인할 수 있었다.
- 방향에 대한 정보
행렬식의 부호는 선형 변환 후 방향의 변화에 대한 정보를 가지고 있다.
- 양수인 경우: 임의의 두 벡터 사이의 오리엔테이션(방향성)이 보존되며 오른손 좌표계가 된다.
- 음수인 경우: 임의의 두 벡터 사이의 오리엔테이션(방향성)이 반전되며 왼손 좌표계가 된다.
- 0인 경우: 하위 차원으로 매핑
갑자기 오리엔테이션, 손 좌표계 같은 괴상한 용어가 나와 당황할 수 있지만 차근차근 알아보자.
먼저 양수의 행렬식을 가지는 행렬 $N$ 예시를 가져보자.
$$
N = \begin{bmatrix}
1 & 1 \\
1 & 2
\end{bmatrix},
\textbf{v}_1 = \begin{bmatrix}
1 \\
2
\end{bmatrix},
\textbf{v}_2 = \begin{bmatrix}
4 \\
1
\end{bmatrix}
$$
위 경우를 그림으로 나타내면 다음과 같다.
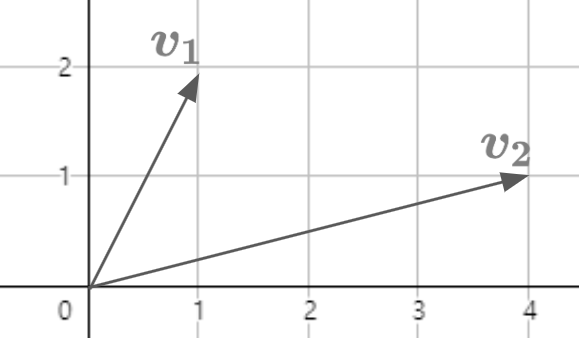
위 상황에서 $\textbf{v}_1$ 은 $\textbf{v}_2$의 반시계 방향에 존재한다. 이 두 벡터를 $N$과 곱한 결과는 다음과 같다.
$$
N\textbf{v}_1 = \begin{bmatrix}
7 \\
11
\end{bmatrix},
N\textbf{v}_2 = \begin{bmatrix}
17 \\
11
\end{bmatrix}
$$

N으로 선형 변환을 취해준 결과도 $N\textbf{v}_1$이 $N\textbf{v}_2$의 반시계 방향에 존재하게 된다.
이것이 오리엔테이션이 보존 된다는 것이다.
그렇다면 행렬식이 음수인 경우도 살펴보자. 아래 $N'$은 행렬식이 -1로 음수이다.
$$
N' = \begin{bmatrix}
1 & 1 \\
1 & -2
\end{bmatrix},
\textbf{v_1} = \begin{bmatrix}
1 \\
2
\end{bmatrix},
\textbf{v_2} = \begin{bmatrix}
4 \\
1
\end{bmatrix}
$$

마찬가지로 $\textbf{v_1}$ 은 $\textbf{v_2}$의 반시계 방향에 존재한다. 이 두 벡터를 $N'$과 곱한 결과는 다음과 같다.
$$
N'\textbf v_1 = \begin{bmatrix}
3 \\
-3
\end{bmatrix},
N'\textbf v_2 = \begin{bmatrix}
5 \\
2
\end{bmatrix}
$$

이 경우 $N'\textbf v_1$은 $N'\textbf v_2$의 시계 방향에 존재한다. 이렇게 둘 사이의 방향이 바뀌는 것이 오리엔테이션이 바뀐다는 것을 의미하게 된다.
0인 경우에 대해서 알아보자. 아래와 같이 Determinant가 0인 $M$이라는 행렬이 존재한다고 하자.
$$
M = \begin{bmatrix}
2 & 4\\
2 & 4
\end{bmatrix}
$$
이 행렬에 임의의 벡터를 곱해보자.
$$
\begin{bmatrix}
2 & 4\\
2 & 4
\end{bmatrix} \begin{bmatrix}
3 \\
1
\end{bmatrix} = \begin{bmatrix}
10 \\
10
\end{bmatrix} \\
\begin{bmatrix}
2 & 4 \\
2 & 4
\end{bmatrix} \begin{bmatrix}
1 \\
-2
\end{bmatrix} = \begin{bmatrix}
-6 \\
-6
\end{bmatrix} \\
\begin{bmatrix}
2 & 4 \\
2 & 4
\end{bmatrix} \begin{bmatrix}
x_1 \\
x_2
\end{bmatrix} = \begin{bmatrix}
2x_1 + 4x_2 \\
2x_1 + 4x_2
\end{bmatrix}
$$
2차원의 점들을 전부 $y=x$의 직선 위로 매핑하게 되는 것을 수식만으로도 알 수 있으며 이는 하위 차원으로 매핑하는 것을 나타낸다.
이번 장에서는 가우스 조던 소거법과 역 행렬 공식의 증명, 역 행렬의 특성 및 역 행렬 존재 조건과 determinant에 대해서 그리고 determinant의 특성과 기하학적인 특성에 대해서 알아보았다.
Reference
'공부 및 정리 > 선형대수학' 카테고리의 다른 글
| 고윳값 분해 (1) | 2023.10.02 |
|---|---|
| 최소 자승법 (0) | 2023.10.02 |
| 행렬의 특성과 특별한 행렬과 벡터 (0) | 2023.09.29 |
| 행렬과 벡터의 기초 연산 (0) | 2023.09.25 |
| 행렬과 벡터의 기초 (0) | 2023.09.25 |



