PCA는 학교 선형대수학 수업에서는 많이 다루지는 않지만 고윳값 분해의 가장 널리 알려진 응용이고 또 요즘 유행하는 딥러닝, 데이터 과학에서 절대로 빼놓을 수 없는 주제이기에 정리를 해보려 한다.
PCA(Principal Component Analysis)란?
PCA… 주 성분 분석… 이름은 엄청 자주 들어봤는데 이게 정확히 뭔지. 그리고 어떤 과정으로 이루어지는 지에 대해서는 잘 이해를 못하고 넘어갔었다.
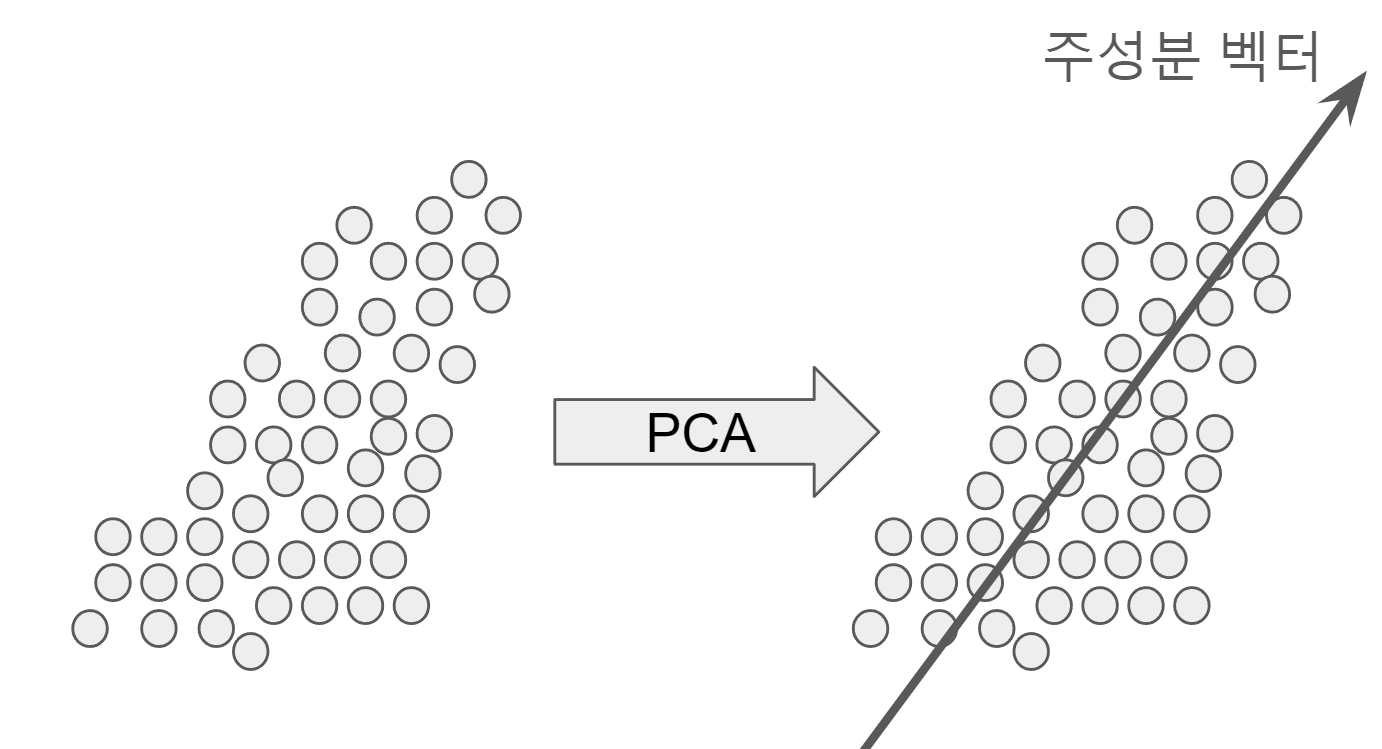

PCA란 주어진 데이터들로부터 이 데이터 분포의 평균으로부터 데이터의 분포를 가장 잘 설명하는 방향인 주 성분 벡터를 찾는 것이 PCA의 주된 목표이다.
이렇게 주어진 데이터의 분포를 가장 잘 설명하는 벡터를 찾게 된다면 이 벡터 한 차원으로 모든 데이터를 정사영 시켜 전체적인 데이터 분포를 표현할 수 있다는 것이고, 이것이 PCA가 차원 축소 기법이라 불리는 이유이다.
그렇다면 분포를 가장 잘 설명하는 방향을 어떻게 구할까? 대부분의 블로그 글들을 보면 데이터의 분포를 가장 잘 설명하는 방향은 데이터의 분산이 가장 큰 방향이라고 써있고, 그 다음으로 잘 설명하는 방향은 가장 잘 설명하는 방향의 수직이다라고 쓰여있다.
그렇다면 여기서 2가지 의문이 생긴다.
- 왜 데이터를 가장 잘 설명하는 방향이 분산이 가장 큰 방향일까?
- 왜 두번째로 가장 잘 설명하는 방향은 첫번째 방향에 수직할까?
이것들을 해결하기 위해서 먼저 데이터를 가장 잘 설명한다는 것을 정의하는 것이 중요하다.


먼저 기본적으로 분포는 위와 같은 그림처럼 평균이 원점이 아닌 분포로 되어있을 것이다.
여기서 데이터의 x, y 좌표 평균을 모든 데이터에 빼주어 평균이 원점이 되도록 만들어주자.

여기서 데이터를 가장 잘 설명한다는 것은 어떤걸 의미할까?

이렇게 데이터를 벡터 위로 정사영시 없어지는 정보(파란 직선)가 가장 적은 방향을 말할 것이다.
이를 모든 점에 대해서 적용시 아래 식을 최적화 해야 함을 알 수 있다.
$$
\begin{matrix}
\min_u \frac{1}{N}\sum^N_i (d_i - d_i^Tu \cdot u)^T(d_i - d_i^Tu \cdot u) \\
\text{s.t. }||u||^2_2 = 1 = u^Tu
\end{matrix}
$$
위 식을 가장 작게 만드는 $u$를 찾는것이 우리의 목표다.
위 식을 만드는 과정은 합리적이다. 그렇다면 위에서 말한 궁금증은 어떻게 발생하는 것일까?
위 식을 풀면 위에서 품었던 의구심들을 해결할 수 있다.
위 식을 풀어쓰면 다음과 같다.
$$
\min_u \frac{1}{N}\sum_i (d_i^Td_i - d_i^Tu\cdot u^Td_i - d_i^Td_i^Tu\cdot u + d_i^Tu \cdot u^Td_i^Tu \cdot u)
$$
위 식에서 가장 앞의 $d_i^Td_i$는 u와 관련 없으므로 제거할 수 있다.
맨 뒤의 식 $d_i^Tu \cdot u^Td_i^Tu \cdot u$에서 $d_i^Tu$는 scala이므로 앞으로 뺴주면 $d_i^Tu\cdot d_i^Tu \cdot u^T u$인데 $u^Tu = 1$이므로 $d_i^Tu\cdot d_i^Tu$가 된다. 이는 뒤에서 두번째 식 $d_id_i^Tu\cdot u = d_i^Tud_i^Tu$이므로 둘이 사라지게 된다.
즉, 정리하면 아래와 같다.
$$
\min_u \frac{1}{N}\sum_i (-d_i^Tu\cdot u^Td_i)
$$
여기서 $u^Td_i$는 scala이므로 앞으로 빼 줄 수 있다.
$$
\min_u \frac{1}{N}\sum_i (-u^Td_id_i^Tu)
$$
$d_i$는 기존 데이터 포인트 $d$에서 평균을 빼준것이라 했으므로, $d_i = (d_i - \bar d )$이다.
위 식은 결국 다음과 같다.
$$
\min_u \frac{1}{N}\sum_i (-u^T(d_i - \bar d)(d_i - \bar d)^Tu)
$$
$\frac{1}{N}\sum$을 안으로 가져오면 아래와 같다.
$$
\min_u -u^T \sum_i\frac{(d_i - \bar d)(d_i - \bar d)^T}{N}u = -u^TR(d)u
$$
위 식에서 $\sum_i\frac{(d_i - \bar d)(d_i - \bar d)^T}{N}$이 식은 어디서 많이 본 수식이다. 바로 분산을 구하는 공식이다. 여기서는 행렬이기 때문에 위 결과는 Covariance Matrix가 되게 된다.
위 식은 결국 다음과 같다. (-1을 곱해 maximize)
$$
\begin{matrix}
\max_u u^TR(d)u \\
\text{s.t. } ||u||^2_2 = 1 = u^Tu
\end{matrix}
$$
위 식은 라그랑지안 최적화를 통해 최적화가 가능하다.
$$
L = u^TR(d)u + \lambda(1 - u^Tu)
$$
이를 u에 대해 미분을 해주면,
$$
\begin{align}
dL_u &= du^TR(d)u + u^TR(d)du - \lambda du^Tu - \lambda u^Tdu \\
&= 2u^TR(d)du - 2\lambda u^Tdu \\
&= (2u^TR(d) - 2\lambda u^T)du \\
&= \frac{dL}{du^T}du
\end{align}
$$
행렬을 벡터로 미분하는것은 $u$의 모든 요소로 미분을 하나하나 다 해주면 된다. $\begin{bmatrix} \frac{dL}{du_1}, \frac{dL}{du_2}, \dots\end{bmatrix}$
여기서 $\frac{dL}{du^T} = 0$인 $u$를 찾으면 끝이다. 이에 맞게 정리하면 아래 꼴이 된다.
$$
u^TR(d) =\lambda u^T
$$
이때 $R(d)$는 symmetric 행렬이다. 위 식은 고윳값 분해 때 지겹도록 본 그 식의 형태와 동일하다는 것을 알 수 있다.
즉, $u$는 $R(d)$의 eigen vector이고, $\lambda$는 eigen value이다. 이때 $R(d)$는 symmetric이므로 언제나 대각화 가능하며 orthogonal matrix로 분해 가능하다는 성질도 알고 있다.
$$
\begin{matrix}
\max_u u^TR(d)u \\
\text{s.t. } ||u||^2_2 = 1 = u^Tu
\end{matrix}
$$
다시 돌아와서 우리는 위 식을 최적화 해야한다. 이때 $R(d)$를 eigen value와 vector로 다시 나타내면 다음과 같다.
$$
u^T(\lambda_1q_1q^T1 + \lambda_2q_2q^T2 + \dots)u
$$
아까 우리는 $u$도 $R(d)$의 eigen value라 했으므로 $u$는 $q_i$ 중 하나가 된다.
그렇다면 $i$번째 $q$가 $u$라면 다른 $q$들과는 orthogonal한 상태가 되므로 우리는 eigen value가 가장 큰 $q$를 찾아야 하기에 u는 $q_1$이 될 것이고, 그 다음으로 설명을 잘하는 주성분 벡터는 $q_2$가 될 것이며 이는 첫번째 벡터 $q_1 =u$와 수직한다.
다시 문제들을 살펴보자.
- 왜 데이터를 가장 잘 설명하는 방향이 분산이 가장 큰 방향일까?
- 왜 두번째로 가장 잘 설명하는 방향은 첫번째 방향에 수직할까?
먼저 1번은 우리가 식을 전개하다 보니 covariance matrix가 나왔고, 이것이 포함된 식을 목적에 맞게 최적화 하려 보니 설명을 잘한다 가정한 벡터 $u$는 이 covariance matrix의 eigen vector라는것을 알려주는 식을 얻을 수 있었다. 이때 다시 최적화 식을 분해해 보니 $u$는 covariance의 가장 큰 eigen vector가 된다는 것을 알 수 있었기에 이 벡터가 가장 분산이 큰 방향인 것을 알 수 있다.
그 다음으로 2번은 위에서 말한 것처럼 $u$는 covariance의 eigen vector 들 중 하나가 되어야만 한다. 이때 각 eigen vector들은 covariance가 symmetric 행렬이므로 수직하게 만들 수 있고, 이 때문에 그 다음으로 설명을 하는 벡터들은 첫번째 벡터에 수직하게 된다.
또한 이렇게 분산이 큰 몇 개의 벡터를 축으로 데이터를 나타낼 수 있기에 차원 축소 기법이라 볼 수 있는것이다.
PCA와 Eigen Decomposition의 다른점
둘 다 데이터를 압축하는 방식이지만 차이점이 존재한다.
PCA의 경우 여러 개의 데이터 분포가 있을 때 이들을 적은 차원으로 표현하는 방식이라 볼 수 있고, Eigen Decomposition은 한개의 데이터가 있을때 이를 rank-1 matrix들로 쪼개서 이들의 합으로 표현하므로 데이터 1개의 용량을 축소하는 방식이라 볼 수 있다.
즉, PCA는 여러 개의 데이터 분포가 필요하지만, Eigen Decomposition은 한 개의 데이터에도 적용할 수 있는 방식이다.
PCA의 응용
보통 PCA의 응용하면 얼굴과 관련된 내용들이 많다. ㅋㅋ 아마도 특징 추출이 PCA로 쉬워서인듯 하다.

위와 같은 올리베티라는 사람의 얼굴 데이터셋에서 PCA를 통해 특징을 추출한다.
이렇게 얻은 PCA 벡터들 중 가장 설명력이 높은 2개 벡터와 평균을 함께 서로 다른 가중치의 선형 조합을 하면 아래와 같이 그럴듯한 얼굴들이 나오게 된다.


그 외의 간단한 응용으로 안경 제거를 할 수 있다고 한다.
얼굴 이미지 분포에서 안경이 있는 데이터에서 안경을 제거하고 싶은 경우, eigen face를 전체 데이터에서 추출 후 하고 싶은 데이터를 eigen face로 근사를 한다. 이를 1의 이미지에서 뺴 준 값에서 임계치 이상인 영역을 1에서 평균 값으로 대체한다. 이를 반복해주면 안경이 없는 이미지를 얻을 수 있다고 한다. ㅋㅋ
이러한 응용들은 Auto Encoder와 비슷한 것 같다. 차원을 축소하는것도 그렇고, 데이터를 생성하는 것도 그렇고, noise를 제거(위에서 안경)하는 부분도 그렇고…
https://youtu.be/C21GoH0Y9AE?si=I7sNkihsTUYzzN4Z
위 영상을 보면 AE의 간단화된 버전(선형)이 바로 PCA라고 한다.
드디어 PCA도 끝났당
Reference
'공부 및 정리 > 선형대수학' 카테고리의 다른 글
| Matrix Inversion Lemma (1) | 2023.12.11 |
|---|---|
| Sherman-Morrison formula와 RLS (1) | 2023.12.11 |
| 유사 행렬 (Similar Matrix) (1) | 2023.10.29 |
| 행렬의 여러가지 분해 (1) | 2023.10.29 |
| 그람-슈미트 직교화 (Gram-Schmidt Orthogonalization) (0) | 2023.10.29 |

