2부 소개
- 이제부터는 현대 딥러닝의 현황에 대해 정립한다. 본 파트에서는 현 세대 심층 학습의 거의 모든 응용이 의존하는 parametric function approximation 기술들에 대해 정리하고, 그러한 함수를 표현하는 데 사용하는 Deep Feedforward Network을 설명한다. 그 후 regularization과 optimization을 위한 고급 테크닉을 소개한다. 또한 고해상도 이미지와 긴 시계열과 같은 입력을 위한 특수화된 신경망인 CNN과 RNN에 대해서 소개하고 마지막으로 딥러닝이 관여하는 응용프로그램의 설계 구축 설정을 위한 방법론과 실제 응용 사례를 소개한다.
- 이전까지는 딥러닝을 학습하기 위해 필요한 수학적 지식과 기타 요소들에 대해 학습하였다.
Deep Feedforward Network는 딥러닝의 정수로 MLP(다층 퍼셉트론)이라고도 부른다. MLP의 목표는 특정 함수 $f^\ast$를 근사하는 것이다. 예를 들어 classifier의 경우 $y=f^\ast(x)$는 입력 $x$를 출력 $y$로 분류하고, MLP는 $y=f^\ast(x;\theta)$를 정의하고 파라미터 $\theta$를 함수 $f^\ast$을 최적으로 근사하도록 학습한다. 이 Feedforward Network는 여러 신경망의 기초가 되는 모델로 매우 중요하게 짚고 넘어가야 한다.
이때 Feedforward라는 의미는 입력의 흐름이 앞쪽으로만 간다는 의미이다. 즉, feedback이 없다는 의미이다.
Network라는 것은 여러 다른 함수들이 그물처럼 엮인 형태로 표현된다는 것이다. 예를 들어 $f^{(1)}, f^{(2)}, f^{(3)}$라는 함수들이 연쇄적으로 적용되는 경우 $f^{(3)}(f^{(2)}(f^{(1)}(x)))$와 같이 chain 구조로 표현되는데 이러한 chain 구조가 신경망의 구조에서 가장 흔하게 쓰이는 형태이다. 이때 첫 번째 함수 $f^{(1)}$를 네트워크의 first layer라 부르며 $f^{(2)}$는 second layer라 부른다. 이때 각 함수들을 layer라 부르며 이렇게 연쇄적으로 적용되는 함수의 개수를 network의 depth라 부른다. (이로부터 Deep이라는 용어가 비롯된 것이다.) 마지막으로 Feedforward Network의 마지막 층은 출력이 나오는 층으로 output layer라 부른다.
신경망을 훈련하는 것은 $f^\ast(x)$에 근사하는 것이며 train data는 각 점에서 출력 값 $f^\ast(x)$를 지정해준다. 이때 output layer에서 나온 값은 train data의 출력 값과 반드시 같아야만 한다. 이렇게 output layer의 출력은 명시적으로 알려주지만, 중간 layer의 출력은 알려주지 않는데, 이러한 출력은 학습 알고리즘이 결정한다. 이렇게 출력이 train data가 알려주지 않기 때문에 이러한 출력을 내는 layer들을 hidden layer라 부른다.
마지막으로 neural의 의미는 이 구조가 신경 과학에서 영감을 얻었기 때문이다. 일반적으로 Feedforward Network의 각 hidden layer는 벡터를 입력으로 받아 벡터를 출력하게 되는데 이러한 벡터의 차원은 신경망의 width에 해당한다. 이때 hidden layer의 작동 방식을 뇌의 뉴런의 작동 방식에 비유할 수 있다. hidden layer를 벡터 대 벡터 함수가 아닌 병렬로 작동하는 unit으로 구성된 layer라 보는 경우 벡터를 입력 받아 scala 값(unit)을 출력하는 함수로 볼 수 있고, 각 unit은 여러 단위의 출력들로 이루어진 입력을 받아 activation을 계산한다는 측면에서 뉴런과 비슷하다 할 수 있다.
하지만 현대 딥러닝 연구는 신경 과학 뿐만 아니라 수학과 공학의 여러 분야에서 영향을 받고 있고, 무엇보다 신경망의 목표는 생물학적 뇌를 모방하는 것이 아닌, 통계적 일반화를 위해 고안된 function approximation machine으로 생각하는 것이 현재는 더 올바르다.
Feedforward Network를 선형 모델의 한계를 극복해냈다는 점을 중심으로 이해하는 방식도 생각해 볼만 한다. 선형 모델들은 closed form 또는 convex 최적화를 통해 효율적으로 최적화를 할 수 있다는 점이 매력적이지만 이러한 선형 모델들은 선형 함수들에만 capacity가 있다는 한계점이 있기에 임의의 두 변수 사이의 상호작용을 이해하지 못한다는 한계가 존재한다. 이러한 선형 모델을 $x$의 비 선형 함수들을 확장하는 방법은 선형 모델을 x가 아닌 변환된 입력 $\phi(x)$에 적용하는 것이다. (이때 $\phi$는 비 선형 변환)
이때 문제는 $\phi$가 무엇이 되어야 하는가? 이다.
- 첫 번째 접근 방식은 RBF와 같은 general kernel trick을 사용해 무한 차원으로 보내는 것이다. $\phi$의 차원이 충분히 높으면 모델은 항상 train set에 fit하기에 충분한 capacity를 가진다. 하지만 test set에 대한 generalization은 나쁜 경우가 많다.
- 두 번째 접근 방식은 general 보다는 specific한 kernel trick을 사용하는 것으로 딥러닝 이전에는 이게 주류였다. 이를 위해서는 개별 과제들마다 엄청난 노력이 쏟아져야 했다. 예를 들어 음성 인식과 컴퓨터 비전과 같은 다른 영역에는 서로 다른 특화된 지식이 필요했다.
- 마지막 접근 방식은 딥러닝의 전략으로 $\phi$를 배우는 것이다. 이 방식에서 모델은 $y=f(x;\theta, w) = \phi (x;\theta)^\top w$ 이다. 이 식에서는 적절한 $\phi$를 배우기 위한 $\theta$와 적절한 mapping을 위한 $w$를 학습한다. 이때 $\phi$는 hidden layer를 정의하며, 문제에 convexity가 있는 경우 실패하는 경우는 이 마지막 방법 뿐이다.
- 하지만 이 방식은 $\phi(x;\theta)$로 표현은 parametrize하고, 적절한 표현을 위한 $\theta$를 최적화 한다. 이때 필요한 경우 아주 다양한 함수를 포괄하는 function family $\phi(x;\theta)$를 사용하면 되며, 또한 specific한 kernel trick을 사람이 고안할 필요 없이 그럴 가능성이 있는 general function familiy를 지정하기만 하면 된다는 1, 2를 아우르는 아주 큰 장점이 있다.
이렇게 feature의 학습을 통해 모델을 개선한다는 원리는 딥러닝에서 계속 등장하는 원리이다.
XOR 예제
XOR 함수는 두 이진수 입력을 받아 정확히 하나가 1과 같은 경우에만 1을 리턴하며, 그 외의 경우에는 0을 리턴하는 함수이다. 예제를 간단히 만들기 위해 $\mathbb X = {[0,0]^\top, [1,0]^\top,[0,1]^\top,[1,1]^\top}$를 입력으로 받고, $y = f(x;\theta)$를 이러한 함수로 근사하는 것으로 제한한다.
이 문제의 접근 방식은 이 문제를 간단한 회귀 문제로 간주해 MSE를 손실 함수로 사용하는 것이다.
$$
J(\theta) = {1\over 4}\sum_{x\in \mathbb X}(f^\ast (x) - f(x;\theta))^2
$$
우리의 모델 $y = f(x;\theta)$를 다음과 같이 선형 모델로 정의하자. ($\theta$는 $w$와 $b$로 이루어짐)
$$
f(x;w,b) = x^\top w+b
$$
normal equation을 이용해 위를 풀면, $w = 0, b = {1\over 2}$를 얻는다. 즉, 선형 모델은 언제나 0.5의 출력을 내게 된다. 왜 이럴까? 아래 그림의 왼쪽 그림은 선형 모델이 왜 XOR 함수를 표현이 불가능 한지에 대해 알려준다. 이러한 문제를 풀기 위해서는 오른쪽과 같은 해법을 표현할 수 있는 다른 feature space를 배워야 한다.

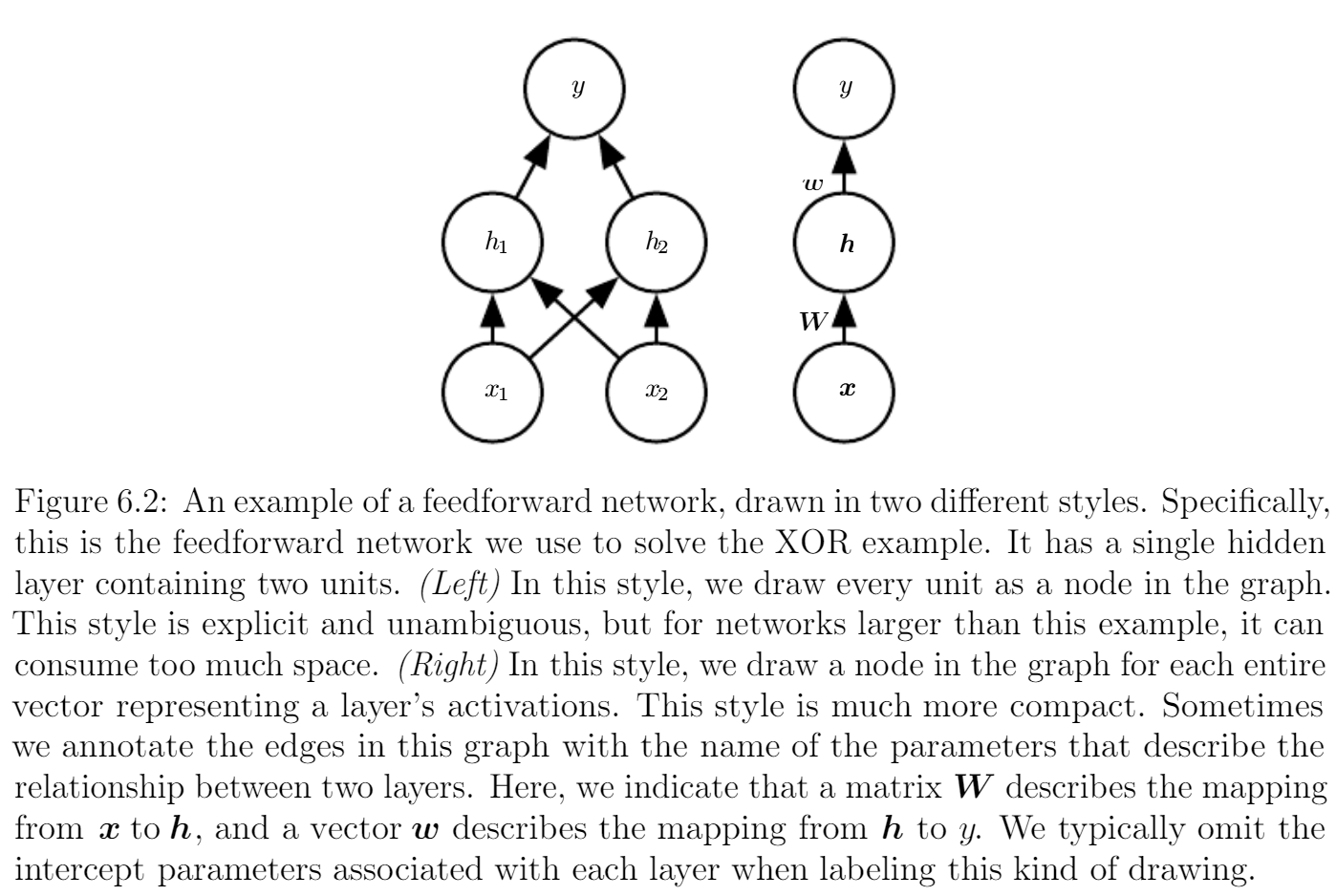
위 그림과 같이 hidden unit이 2개 있는 하나의 hidden layer를 도입해 이를 해결 가능하다. 첫 hidden layer $h$에서 새로운 feature space로 mapping하며 이것이 기존 함수의 입력으로 들어가게 된다. (이전과 다른 점은 똑같은 선형 회귀 모델이 기본 입력이 아닌 $h$의 space로 매핑된 결과를 입력으로 받는 것)
이를 chain 구조로 표현하면 $f^{(2)}(f^{(1)}(x)) = f(x;W,c,w,b), ~ h = f^{(1)}(x;W,c), ~ y = f^{(2)}(h;w,b)$가 된다.
이제 문제는 $f^{(1)}$을 어떻게 두어야 할 지이다. 이전처럼 선형으로 두게 되는 경우 $f^{(1)} = W^\top x$가 되고, 결국 $f^{(2)}(f^{(1)}(x)) = w^\top W^\top x = w'x ,(w' = w^\top W^\top)$로 두 번 함수를 적용하는 의미가 없다. 그러므로 비 선형 함수로 두어야만 한다. 대부분의 신경망은 학습된 파라미터를 통한 affine 변환 이후 고정된 비 선형 함수를 적용해 비 선형성을 추가한다. 이때 비 선형 함수를 activation function이라 부른다. 즉, $h = g(W^\top x + c)$ 와 같이 표현된다.
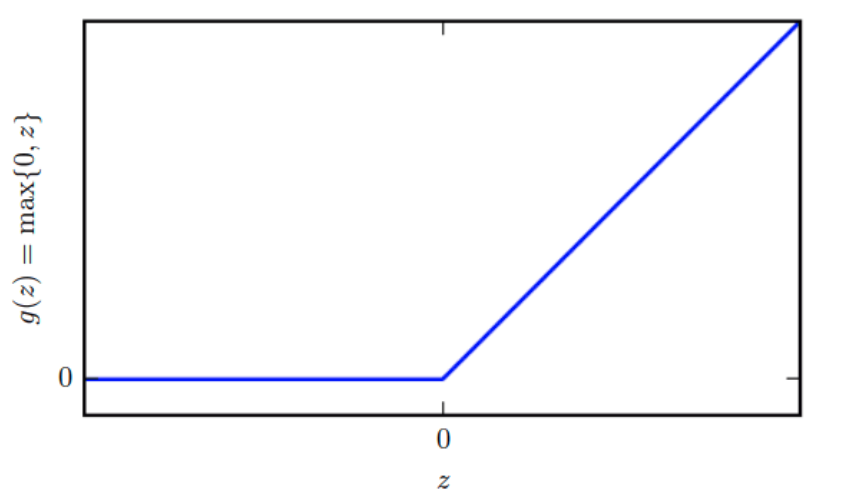
보통 이때 사용하는 활성화 함수 $g$는 ReLU가 권장되는데, 이는 $g(z) = \max(0,z)$로 정의된다.
이제 전체 신경망을 다시 써보면 아래 식과 같다.
$$
f(x;W,c,w,b) = w^\top \max(0, W^\top x + c) + b
$$
이렇게 정의한 경우 solution은 다음과 같다.
$$
W = \left[
\begin{matrix}
1 & 1 \
1 & 1 \
\end{matrix}
\right], ~ c = \left[
\begin{matrix}
0 \
-1 \
\end{matrix}
\right], ~ w = \left[
\begin{matrix}
1 \
-2 \
\end{matrix}
\right], ~ b = 0
$$
이를 실제로 풀어보면 $Wx + c$를 통해 한 직선 위로 이동했다가 ReLU를 통해 6.1의 오른쪽 그림처럼 변환되어 선형 모델로 해결이 가능한 것을 확인이 가능하다.
Gradient-Based Learning
신경망 설계는 다른 gradient-based learning 머신러닝 기법들과 크게 다르지는 않다. 가장 큰 차이점은 신경망은 비 선형 함수이기에 볼록 함수를 손실 함수로 사용하기 적합하지 않을 때가 존재한다는 점이다. 보통 신경망에서는 선형 회귀와 같은 연립 방정식 해법이나 로지스틱 회귀, SVM에서 사용하는 볼록 함수 최적화 알고리즘 대신 cost function의 값을 낮추는 반복 gradient based 최적화를 사용한다. 볼록 함수의 경우 임의의 점에서 시작한 최적화가 보장이 되지만 비 볼록 함수에 stochastic gradient descent를 적용한 경우 보장이 되지 않고, 초기 파라미터에 민감하게 반응한다. 그렇기에 Feedforward Network는 초기 가중치 파라미터를 작은 난수 값으로 초기화 하는 것이 중요하다. (bias는 작은 음이 아닌 난수) 이러한 부분은 8장에서 자세히 다룬다.
Cost Function
Cost Function을 정하는 것은 딥러닝 설계에서 매우 중요하다. 다행히, 신경망에서 사용하는 Cost function들은 linear 모델의 Cost Function과 비슷하다. 보통 모델들은 분포 $p(y|x;\theta)$를 정의하고, MLE를 적용하여 훈련한다. (즉, cross entropy를 cost function으로 사용한다는 것) 물론 때에 따라서는 전체 확률 분포 대신 그냥 $x$를 조건으로 한 $y$의 어떤 통계량을 예측하는 좀 더 단순한 접근 방식을 사용할 때도 존재한다. 추가적으로 전체 cost function은 여기에 regularization을 더한다.
Learning Conditional Distributions with Maximum Likelihood
현대 신경망은 MLE를 통해 학습한다. 이는 cost function이 negative log-likelihood라는 것이며, 이는 train data와 model distribution 사이의 cross entropy라 할 수 있다.
$$
J(\theta) = -\mathbb E_{x,y\sim \hat p_{data}}\log p_{model}(y|x)
$$
구체적인 형태는 $p_{model}(y|x)$을 어떻게 정의되는지 따라 다르다. MLE의 관점에서는 모델 $p(y|x)$가 결정되는 경우 cost function $\log p(y|x)$가 자동으로 결정되어 이러한 cost function의 설계에 대한 부담이 없다는 장점이 있다.
cost function의 기울기가 학습 알고리즘을 잘 지도 할 수 있을 정도로 크고 예측 가능해야 한다는 것은 신경망 설계에서 자주 등장하는 주제이다. saturate 되는 activation function의 경우 cost function의 기울기가 아주 작아지기 때문에 이와 정 반대된다. 이럴 때 negative log-likelihood는 빛을 발할 수 있다. output unit에 exp function이 있는 경우 아주 큰 음의 값에서 saturate되는데 log는 exp를 상쇄해 이를 해결 가능하다.
MLE를 하는 경우 cross entropy의 최솟값을 찾기 어렵다는 성질이 있다. 로지스틱 회귀의 경우 정확한 확률값 0, 1을 표현하지 못하고 두 극단에 극한으로 가까워지는 형태를 가진다. real-value를 출력하는 변수들의 경우 만약 모델이 출력 분포의 밀도를 조절 가능한 경우 (예를 들어 가우시안 출력 분포의 variance를 학습한 경우) 맞는 training set에 매우 밀집하게 되어 cross entropy가 음의 무한에 가까워지게 된다. (이 부분이 이해가 안감… cross entropy가 음이 될 수 있는가? 여기서는 아니라구 하는뎅…) 이는 regularization을 이용해 방지할 수 있다. (7장에서 다룬다)
Learning Conditional Statistics
앞서 말한 것처럼 전체 확률 분포 $p(y|x;\theta)$를 배우는 것이 아닌 $x$가 주어졌을 때 $y$의 한 조건부 통계만 배우면 되는 경우가 있다.
예를 들어 $y$의 평균을 예측하는 $f(x;\theta)$를 원할 수 있다. 만약 충분히 강력한 신경망은 다양한 함수를 표현할 능력을 갖추었으며, cost function을 funtional이라 볼 수 있다.
functional이란 함수를 정의역으로, 실수를 치역으로 갖는 함수이다. 비용 함수를 functional로 간주하면, 학습이라는 것을 특정 형태의 함수의 매개 변수 구성을 선택하는 것이 아닌 함수 자체를 선택하는 것으로 생각할 수 있다. 즉, cost functional을 설계할 때에는 최솟값이 나오는 함수를 선택해야 한다. 위의 평균을 예측하는 예시에서는 평균과의 차이가 최솟값이 나오는 cost functioal을 선택하게 된다.
calculus of variations(19장에서 배우는 함수에 대한 최적화를 위한 수학적 기법)을 사용해 결과를 유도하면 다음과 같다.
$$
f^* = argmin_f \mathbb E_{x, y \sim P_{data}} || y - f(x)||^2
$$
이 최적화 문제를 풀면 다음과 같다.
$$
f^*(x) = \mathbb E_{y\sim p_{data}(y|x)}[y]
$$
즉, MSE를 최소화하여 $x$의 각 값에 대한 $y$의 평균을 예측 가능하다는 의미이다.
calculus of variations를 이용해 또 다른 결과를 유도하면, 다음과 같이 y의 median을 예측하는 함수라는 것이다. 이러한 비용 함수를 MAE(mean absolute error)라 부른다.
$$
f^* = argmin_f \mathbb E_{x,y\sim p_{data}}||y-f(x)||_1
$$
즉, MSE와 MAE를 이용해 학습한다면 y의 평균에 대해 예측하는 함수를 근사할 수 있다.
아쉽게도 MSE와 MAE는 gradient 기반 최적화와 함께 사용 시 성능이 나쁜 경우가 많다. 이는 output unit이 saturate해 gradient vanishing이 발생하기 때문이다. 이는 전체 확률 분포 $p(y|x)$를 평가하지 않을 때에도 cross entropy를 더 흔히 사용하는 이유이다.
Output Units
Cost function의 선택은 output unit과 밀접하게 연관되어 있다. 대부분 데이터의 분포와 모델의 분포의 cross entropy를 cost function으로 사용하는데, 이러한 cross entropy의 형태는 출력의 표현 방식에 따라 달라진다. output layer에서는 특징들을 적절히 변환해 신경망이 풀어야 할 과제를 만족하는 출력을 내야만 한다. 이러한 출력의 표현 방식들에 대해 알아보도록 하자.
Linear Units for Gaussian Output Distributions
간단한 출력 예시로 affine 변환에 기초한 비 선형성이 없는 출력 단위를 하나 살펴보자. 이런 종류의 출력 단위들을 그냥 linear units라고 한다. 이런 Linear units으로 출력 단위가 주어진 output layer는 $\hat y = W^Th + b$이다. Linear output layer는 보통 조건부 가우시안 분포의 평균을 산출하는 용도로 흔히 사용한다.
$$
p(y|x) = \mathcal N(y;\hat y, I)
$$
이 경우 log-likelihood를 최대화 하는 것은 MSE를 최소화 하는 것과 같다.
이런 Maximum likelihood를 사용하면, 가우시안 분포의 공분산을 바로 학습 가능하며, 가우시안 분포의 공분산을 입력의 함수로 만드는 것도 가능하다. 그러나 이 공분산은 모든 입력에 대해 positive definite이어야 한다는 제약 조건이 있고, 이는 linear output layer로는 만족하기 어렵기에 공분산 행렬을 parameterize할 때에는 보통 비선형 output unit을 사용한다. ← 먼 말이징…
linear units는 잘 saturate하지 않기 때문에 gradient 기반 최적화에 큰 문제가 되지 않으며, 그 외 여러 최적화 알고리즘과도 잘 작동한다는 장점이 있다.
Sigmoid Units for Bernoulli Output Distributiopns
딥러닝의 Task들은 이진 변수 $y$의 값을 예측하는 경우가 많다. 이러한 Task에 Maximum Likelihood를 적용하는 경우 $x$가 주어졌을 때의 $y$에 관한 Bernoulli distribution으로 정의한다.
Bernoulli distribution은 하나의 scala로 정의되며, $P(y = 1|x)$만 예측하면 되며 구간은 $[0,1]$을 만족해야만 한다. 이러한 제약을 만족하기 위해 Linear Unit 하나로 출력이 이루어지는 경우, 이 Linear layer를 아래와 같이 설계해 $[0,1]$ 구간내로 맞출 수 있다.
$$
P(y = 1|x) = \max(0, \min(1,w^\top h+b))
$$
하지만 이런 접근은 결과가 0 이하가 되는 경우 기울기가 0이 되어 더 이상 학습을 진행 할 수 없을 수 있다. 더 나은 접근법은 잘못된 답을 모델이 가질 때 strong gradient를 언제나 가진다고 보장해 주는 것이다. 이 접근법은 sigmoid를 maximum likelihood와 결합하는 것에 기초한다. sigmoid output unit은 아래와 같이 정의된다.
$$
\hat y = \sigma(w^\top h + b)\
\sigma \text{ is logistic sigmoid function}
$$
이렇게 하면 gradient가 0이 되는 일은 없어지며 normalize 되지 않은 확률이 도출된다. (합이 1이 아닌 확률) 이렇게 normalize 되지 않은 로그 확률들이 $y$와 $z$에서 선형인 경우 로그 확률들을 거듭 제곱하면 normalize 되지 않은 확률들이 나온다. 이 확률들을 적당한 상수로 나누어 이를 normalize 하기 위해서 아래와 같이 normalize 해준다.
$$
\log \tilde P(y) = yz,\\
\tilde P(y) = exp(yz),\\
P(y) = \frac{\exp(yz)}{\sum^1_{y'=0} \exp y'z}\\
P(y) = \sigma((2y - 1)z)
$$
이진 변수에 관해 이런 분포를 정의해주는 $z$를 logit이라 부른다. 이런 log space의 확률들을 예측할 때에는 maximum likelyhood 학습과 잘 어울린다. Maximum likelyhood가 사용하는 Cost function이 $-\log P(y|x)$이기 때문에 cost function의 log는 sigmoid의 exp를 제거하는 역할을 하며 sigmoid가 saturate되는 것도 방지해 주기 때문이다.
sigmoid로 parameterize 된 Bernoulli distribution에 대한 maximum likelyhood 학습의 Cost function은 다음과 같다.
$$
J(\theta) = -\log P(y|x)\
= -\log \sigma((2y-1)z)\
=\zeta((1-2y)z)\
(\zeta \text{ is softplus function})
$$
이 손실 함수는 $(1-2y)z$가 매우 작은 경우에만 saturate 하는 것을 마지막 softplus 표현 식으로 알 수 있다. 즉, $y = 1$이고, $z$가 매우 큰 양수이거나 $y = 0$ 이고 $z$가 매우 큰 음수인 경우이다. ($y$는 $[0,1]$ 구간에 존재해야 하므로) 이는 y가 좋은 답을 출력하고 있을 때이므로 딱히 문제가 되지는 않는다. MSE와 같은 손실 함수는 $\sigma(z)$가 saturate할 때 마다 Cost function이 saturate할 수 있고, saturate가 발생한다면, 기울기가 작아져 학습을 할 수 없게 된다. 따라서 sigmoid output unit의 경우 Maximum Likelihood가 적절하다. (cross entropy == Maximum Likelihood)
Softmax Units for Multinoulli Output Distributions
$n$가지 값에 대한 이산 변수에 관한 확률 분포를 나타낼 때에는 보통 softmax를 사용한다. 이 softmax 함수는 이진 변수의 확률을 나타낼 때 쓴 sigmoid 함수의 일반화라 볼 수 있다.
softmax는 보통 $n$개의 다른 class의 확률 분포를 표현하기 위해 classifier의 output에서 자주 사용하며, 아주 가끔씩 모델 내부 hidden unit에서 변수의 n가지 옵션 중에 선택을 해야 하는 경우 사용하기도 한다.
앞서 본 이진 변수의 경우, 다음 식을 통해 single number를 생산해냈다.
$$
\hat y = P(y=1|x)
$$
확률 값이기 때문에 0~1 사이 값이어야 하며, 이 값의 로그가 loglikelihood를 이용한 gradient 기반 최적화와 잘 되어야 하므로, $z=\log \tilde P(y=1|x)$를 구하였다.
위와 같은 접근 방식에서 카테고리의 값이 두 가지가 아닌 임의의 n가지 이산 변수의 경우로 일반화하려면, 요소들이 $\hat y_i = P(y=i|x)$인 벡터 $\hat y$를 구해야 한다. 이때 $\hat y$의 요소의 합이 1이 되어야 하며, 각 값은 0~1 사이의 값으로 mapping 되어야 한다. Bernoulli 분포에서 사용한 일반화를 이 경우에도 사용 가능하다. 먼저 linear layer로 unnormalized log probabilities $z$를 구하자.
$$
z = W^\top h + b\
z_i = \log \tilde P(y = i|x)
$$
이제 softmax를 적용해 $\tilde y$를 얻을 수 있다. 이때 softmax는 다음과 같이 정의된다.
$$
\text{softmax}(z)_i = {\exp(z_i)\over \sum_j \exp(z_j)}
$$
logistic sigmoid에서처럼 exp 함수는 maximum log-likelihood를 이용해 softmax가 $y$를 출력하도록 할 때 잘 작동한다. 이 경우, $\log P(y=i;z) = \log \text{softmax}(z)_i$ 최대화 해야 한다. softmax안의 exp 항은 log-likelihood의 log를 상쇄하는 효과가 있다.
$$
\log \text{softmax}(z)_i = z_i - \log\sum_j\exp(z_j)
$$
위 항의 첫 번째 항인 $z_i$는 cost 함수에 직접적으로 들어간다. 이 항은 saturate 되지 않기 때문에, 두 번째 항의 $z_i$의 기여가 매우 작아져도 학습을 계속 진행할 수 있다. log-likelihood를 최대화 할 때, 첫 번째 항인 $z_i$를 크게 만드려하고, 두 번째 항인 $z$의 summation을 작게 만드려한다. 두 번째 항인 Summation은 $\max_jz_j$로 근사되는데 이러한 근사로부터 negative log-likelihood cost function은 가장 active한 부정확한 예측에 강한 penalty를 부여한다는 직관을 얻을 수 있다.
만약 정답인 $z_i$가 가장 활성화 되어 있다면, $-z_i$와 $\max_j z_j = z_i$가 서로 상쇄되며 train cost에 기여하지 않아 다른 오답인 sample들이 train을 주도하게 된다.
unregularized maximum likelihood는 train set에서 관측한 결과의 정답 비율을 예측하도록 model의 파라미터를 학습 시킨다.
$$
\text{softmax}(z(x;\theta))_i \approx \frac{\sum^m_{j=1} 1_{y^{(j)}=i, x^{(j)}=x}} {\sum^m_{j=1} 1_{x^{(j)}=x}}
$$
maximum likelihood는 consistent estimator(일치 추정기)이기 때문에 model family의 capacity가 train 분포를 표현 할 수 있다면 학습이 보장된다. (실제로는 limited model capacity와 imperfect optimization 때문에 근사 표현만 됨.)
$\exp$를 상쇄 시킬 $\log$가 없는 objective function들은 softmax를 사용 시 $\exp$의 인자가 매우 작은 음의 값이 경우 gradient vanishing이 발생해 학습이 잘 되지 않는 경향이 있다. 이처럼 sigmoid 함수처럼 softmax는 입력 값 간의 차이가 매우 커질 때 saturate된 출력을 내보낸다. 이때 softmax가 saturate 되면 이를 상쇄 시켜줄 능력이 없는 objective function들은 saturate된다. 앞서 4장에서 보았듯이 수치적으로 안정된 softmax는 다음과 같다.
$$
\text{softmax}(z) = \text{softmax}(z - \max_iz_i)
$$
이는 softmax가 최대값과의 차이에만 반응한다는 것을 나타낸다. 입력이 최대값일 때 다른 입력들보다 훨씬 큰 경우 1로 saturate하며 최대값이 아니고 최대값보다 훨씬 작은 경우 0으로 saturate한다. 이는 sigmoid의 일반화라 볼 수 있으며, 이를 해결하지 못하는 cost function은 학습 시 sigmoid 때와 유사한 어려움을 겪는다.
또한 softmax는 승자 독식 구조라는 점을 눈 여겨 볼 만하다. 이는 합이 무조건 1이어야 하기 때문에 하나가 커지면 다른 요소들은 작아질 수밖에 없는 구조이기에 승자 독식 구조이다.
Other Output Types
앞서 본 Linear, Sigmoid, Softmax Output units는 가장 많이 쓰이는 방식이다. 신경망은 우리가 원하는 어떤 종류의 output layer로도 일반화 가능하며, 대부분의 output layer에 대해 maximum likelihood 원리는 좋은 cost function을 설계하는데 매우 효과적이다.
Hidden Units
지금까지 gradient based 최적화로 훈련하는 신경망 설계에 대해 알아보았다. 이젠 Feedforward network의 unique한 주제인 hidden unit의 선택에 대해 알아보도록 하자.
Rectified linear units(ReLU)는 hidden unit으로 아주 적합하다. 하지만 그 외 종류의 hidden unit들이 있으며, 어떤걸 선택할지 결정하는 것은 어려울 수 있다.(대부분 ReLU를 선택하긴 한다.) 이번 절에서는 hidden unit의 motivation에 대한 직관을 얻어보도록 하자.
사실 ReLU와 같은 일부 hidden unit들은 실제로 모든 구간에서 미분 가능이 아닌 경우가 있으며 이는 원칙적으로 gradient based 학습 알고리즘에서 사용할 수 없다. 하지만 실제로는 이러한 모형도 충분히 잘 작동한다. 이는 그러한 미분 불가능한 점에 실제로 도달하지 않는 경우가 대부분이기 때문이다.
그리고 이러한 점은 매우 적기 때문에 실제로 도달한다 하여도 왼쪽 미분, 오른쪽 미분 계수가 둘 다 정의되는 경우가 대부분이기 때문에, 오류를 일으키기 보다는 둘 중 하나를 리턴하며, 이는 어차피 4장에서 본 것처럼 기울기 기반 최적화에는 수치 오류가 발생할 수 밖에 없음을 생각하면 이러한 처리 방식을 이해하고 넘어갈 수 있다. 즉, hidden unit activation function의 미분 불가능 점들은 무시해도 괜찮다.
별 다른 얘기가 없다면 여기서 설명하는 대부분의 hidden unit은 하나의 벡터 $x$를 받아 $z = W^{\top}x + b$를 계산하고, element-wise nonlinear function 함수 $g$를 적용한다.
Rectified Linear Units and Their Generalizations
ReLU는 $g(z) =\max(0, z)$로 정의되며, 이 함수는 linear와 매우 비슷하기에 최적화 되기 쉽다. 이 덕에 unit이 activate되면, 기울기가 1이며, 이계도함수는 거의 모든 영역에서 0으로 계산된다. 이는 기울기의 방향이 second-order 효과들보다 학습에 훨씬 유용하다는 의미이다.
일반적으로 ReLU는 다음과 같이 Affine 변환 후에 적용된다.
$$
h = g(W^\top x + b)
$$
이때 bias $b$는 0.1과 같은 작은 상수로 초기화하지 않으면, ReLU를 통과시 대부분 activate 될 가능성이 있기 때문이다. ReLU에는 한가지 단점이 있다. 활성화 되지 않은 경우 기울기가 0이되어 학습을 할 수 없다는 것이다. 이러한 점을 개선한 ReLU의 variation들이 있다. 이는 활성화되지 않은 경우 기울기를 0이 아닌 $\alpha$를 주는 방식에 기초하였다
- absolute value rectification: $h_i = g(z,\alpha)_i = \max(0, z_i) + \alpha_i\min(0, z_i).$ 보통 이미지에서 물체를 인식하는 신경망에 사용된다.
- leaky ReLU: $\alpha$를 0.01과 같은 작은 값으로 고정함
- parametric ReLU: $\alpha$를 학습 가능한 매개변수로 설정함
- maxout: 입력 $z$를 $k$개의 그룹으로 분할 후 각 그룹의 최대 요소를 출력함
이는 아래 그림처럼 최대 k개의 piece-wise 선형 볼록 함수를 학습할 수 있음 즉, 활성화 함수 자체를 배우는 방식 (자세한 설명은 아래 링크 참조)

[[Part Ⅵ. CNN 핵심 요소 기술] 4. Maxout - 라온피플 머신러닝 아카데미 -
Part I. Machine Learning Part V. Best CNN Architecture Part VII. Semantic Segmentat...
blog.naver.com](https://blog.naver.com/laonple/220836305907)
어쨌든 ReLU와 ReLU의 모든 일반화는 model의 행동 방식이 Linear에 가까울수록 model을 최적화하기 쉽다는 원칙에 기반한다. 같은 원칙을 deep linear network외에도 적용이 가능하다. Recurrent Network를 훈련할 때에는 몇 가지 time step을 통해 정보를 전파하는데 이때 선형 계산이 포함되면 더욱 쉬워진다. 예를 들어 대표적인 Recurrent Network인 LSTM의 경우 summation을 통해 전파하는데 summation은 대표적인 linear activation의 종류이다.
Logistic Sigmoid and Hyperbolic Tangent
ReLU의 도입 전에는 대부분의 신경망은 $g(z) = \sigma(z)$로 표기하는 logistic sigmoid 함수나 $g(z) = \tanh(z)$로 표기하는 hyperbolic tangent 함수를 활성 함수로 사용했다. 이 두 함수는 사실 같다고 할 수 있는데 $\tanh(z) = 2\sigma(2z) - 1$로 표현 가능하다.
이미 output unit에서 확률을 예측하기 위한 용도로 sigmoid unit을 보았던 것처럼 sigmoid는 0 근처를 제외한 대부분의 영역에서 saturate 되며, 0 근처에서는 매우 입력에 민감하다. 이렇게 saturate가 많이 되어있는 함수는 gradient 기반 학습이 어려울 수 있기 때문에 hidden unit으로 사용하는 것은 이제 권장되지 않는다. (물론 이러한 단점을 상쇄 할 수 있다면 사용해도 된다.)
반드시 sigmoidal 활성 함수를 사용해야 하는 경우라면, sigmoid보다는 hyperbolic tangent 함수가 보통 더 좋은 성능을 보이는데 이는 tanh가 0 주변에서 identity 함수와 비슷한 경향을 보이기 때문에 DNN의 activation value들을 작게 유지 할 수 있다면 선형 모형의 훈련과 비슷해져 앞서 말했듯이 더욱 학습이 쉬워지기 때문이다. 이러한 Sigmoidal 활성 함수들은 Feedforward Network 보다는 recurrent network, 확률 모델, autoencoder 등 piece-wise linear activation function을 사용할 수 없는 경우 자주 사용된다.
Other Hidden Units
이외에도 여러 hidden unit들이 있지만 앞서 본 것들 만큼 자주 쓰이지는 않는다. 발표되지 않은 많은 활성화 함수들 중 앞서 본 유명한 함수들 만큼이나 좋은 성능을 보이는 것들이 있다. 예를 들어 본 책의 저자들은 MNIST 데이터에 $h=\cos(Wx+b)$를 사용하는 Feedforward 신경망을 사용했는데 흔히 쓰이는 활성 함수들과 비슷한 정도의 성능을 보였다. 하지만 새로운 활성 함수들은 보통 이전 것들에 비해 눈에 띌 정도로 높은 개선을 보인 경우에만 발표한다. 새로운 hidden unit이 이미 알려진 것들과 비슷한 성능을 보이는 것은 흔하기 때문이다. 독특한 몇 가지에 대해서 만 살펴보도록 하자.
첫 번째로 아예 활성화 함수 $g(z)$를 사용하지 않는 경우가 있다. 이 경우는 그냥 항등 함수를 활성화 함수로 사용한다고 봐도 된다. 하지만 이러한 경우 nonlinearity가 전혀 없기 때문에 이 활성 함수만 사용하는 경우 전체 신경망이 linear하다 볼 수 있다. 하지만 이 활성화 함수를 사용하는 경우에도 이 점이 존재한다. 예를 들어 입력이 $n$개, 출력이 $p$개인 $h=g(W^\top x+b)$를 생각해 보자. 이를 2개의 layer $U$와 $V$를 가중치로 사용하는 layer로 나눌 수 있고, 이를 나타내면 $h = g(V^\top U^\top x+b)$가 된다. 이떄 $U$를 곱해주는 경우 활성화 함수로 항등 함수를 사용한 경우라 할 수 있다. 이때 $U$의 출력이 $q$개 라면, $U$와 $V$의 매개변수의 개수는 $(n+p)q$이다. 이때 $W$가 $np$개라는 것을 생각해보면 매개변수의 개수를 줄일 수 있다는 장점을 가지고 있다. 즉, 선형 활성 함수는 신경망의 매개변수를 줄이는 효과를 제공한다.
또 output unit으로 자주 쓰이는 softmax가 있다. softmax는 가능한 값이 k개인 확률 분포를 나타내어 일종의 스위치로 사용 가능하다. 이러한 종류의 hidden unit들은 메모리 조작을 명시적으로 학습하는 고급 구조만 사용된다.
그 외 소개하고픈 여러 hidden unit은 다음과 같은 것들이 있다.
- Radial basis function (RBF): $h_i = \exp(-{1\over \sigma^2_i}||W_{:, i}-x||^2).$ 이 함수는 $x$가 $W_{:, i}$에 접근함에 따라 점점 더 활성화 된다. 하지만 대부분의 $x$에서 0으로 saturate 되기에 gradient 방식으로는 학습이 어렵다.
- Softplus: $g(a) = \zeta(a) = log(1+e^a)).$ ReLU의 soft한 버전이지만 ReLU가 좀 더 나은 성능을 보인다. 보통 softplus는 권장되지 않으며 hidden unit의 성능이 직관과는 아주 다를 수 있음을 보여준다. 모든 점에서 미분가능하며 포화되지 않아 직관적으로는 ReLU보다 좋을 것 같지만, 경험적으로는 아니었다.
- Hard tanh: $g(a) = max(-1, min(1, a))$ tanh와 ReLU와 비슷하지만 상한과 하한이 있다는 점이 다르다. 또한 1 이상 -1 미만에서는 아예 기울기가 0이 되어버리는 특징이 있다.
Architecture Design
또 다른 신경망 디자인의 중요 포인트는 architecture이다. architecture란 네트워크의 전반적인 구조를 의미한다. (얼마나 많은 unit을 가지고, 어떻게 이 unit들이 연결되는가)
대부분의 신경망은 layer라 불리는 unit의 그룹으로 구성되며, layer들이 아래와 같이 chain 구조로 얽혀있다.
$$
h^{(1)} = g^{(1)}(W^{(1)\top}x+b^{(1)})\
h^{(2)} = g^{(2)}(W^{(2)\top}h^{(1)}+b^{(2)})
$$
이런 chain 기반 architecture의 주된 고려점은 네트워크의 depth와 layer의 width를 결정하는 것이다. 나중에 보겠지만, 사실 train 데이터에 신경망을 fit 하는데에는 은닉층 하나로 충분하지만, 더 깊은, 신경망은 매개 변수의 개수가 매우 적어지고, test set을 일반화 하기 좋다는 장점을 가지며 반대로 최적화하기는 어려운 단점을 가지게 된다. ideal한 구조는 validation set의 error를 기반으로 실험을 거듭해 찾아야 한다.
Universal Approximation Properties and Depth
위 영상을 참고하면 매우 좋다.
matrix multiplication을 통한 linear model들은 많은 cost function들에 적용시 convex function의 최적화 문제가 되어 학습하기 쉽다는 장점이 있다. 하지만 아쉽게도 nonlinear function을 배워야 할 때가 자주 있다.
언뜻 보기에 nonlinear function 학습 시 학습하고 싶은 종류의 nonlinear에 대한 speciallized된 model family가 있어야 할 것 같다. 하지만 운 좋게도 Universal Approximation Theory에 따르면 activation function이 있는 충분한 hidden unit이 있는 hidden layer가 있는 feedforward network가 모든 Borel measureable function에 0이 아닌 오차로 근사 가능할 수 있다. (Borel measureable은 그냥 $\mathbb R^n$의 closed and bounded인 연속 함수 집합이며, feedforward network로 근사 가능이라고 생각하도록 하자. 본 책의 범위를 뛰어 넘음…)
결국 Universal Approximation Theory는 어떤 함수든 큰 MLP로 표현 가능함을 의미한다. 하지만, 학습할 수 있을지에 대해서는 보장되지 않는다. 그 이유는 다음과 같다.
- 학습에 쓰이는 최적화 알고리즘이 원하는 함수에 해당하는 parameter를 찾지 못할 수 있다.
- 과적합 때문에 학습 알고리즘이 다른 함수를 선택할 수 있다.
이전에 No Free Lunch Theory에서 본 것처럼 train set에 없는 점들 또한 generalize한 함수를 선택하게 하는 보편적인 절차는 없다.
Universal Approximation Theory에서는 주어진 함수를 근사하는 충분한 크기의 신경망이 존재하게 된다. 이러한 크기는 말해주지 않는데, Barron은 single layer 신경망으로 근사 시 최악의 경우 hidden unit의 개수가 exponential할 수 있다는 것을 알아냈다. 예를 들어 이진 함수의 경우 $v \in {0,1}$인 $v$에 대해 모든 이진 함수의 개수는 $2^n$이고, 이를 위해서 보통 $O(2^n)$의 자유도가 필요하다. 결국 single layer Feedforward network는 모든 함수를 표현하기에 충분하지만, layer가 엄청나게 크거나 일반화에 실패할 가능성이 있다. 많은 경우 더 깊은 모델을 사용한다면 파라미터의 개수도 줄어들고 일반화 성능도 높아진다.

위 그림은 레이어를 깊게 쌓아감에 따라 decision boundary가 어떻게 변하는지 보여준다. activation function은 절댓값을 사용하였기 때문에 레이어 하나를 지날 때마다 반절씩 접는 것으로 표현하였다. affine transformation은 반절 접는 위치를 정해준다. 레이어를 지날수록 근사해야 하는 함수가 단순해지고, 그렇기 때문에 generalization error가 줄어든다고 볼 수 있다.
(https://leejunhyun.github.io/deep learning/2018/10/26/DLB-06/ 설명)

깊이에 따른 정확도를 나타낸 그림이다. 깊이가 깊어질 수록 더 일반화가 잘되는 특성을 보인다. 물론 model 의 크기가 커진다고 꼭 이러한 특성을 보인다 생각할 수 있지만 아래 그림은 그것에 반하는 특성을 보여준다.
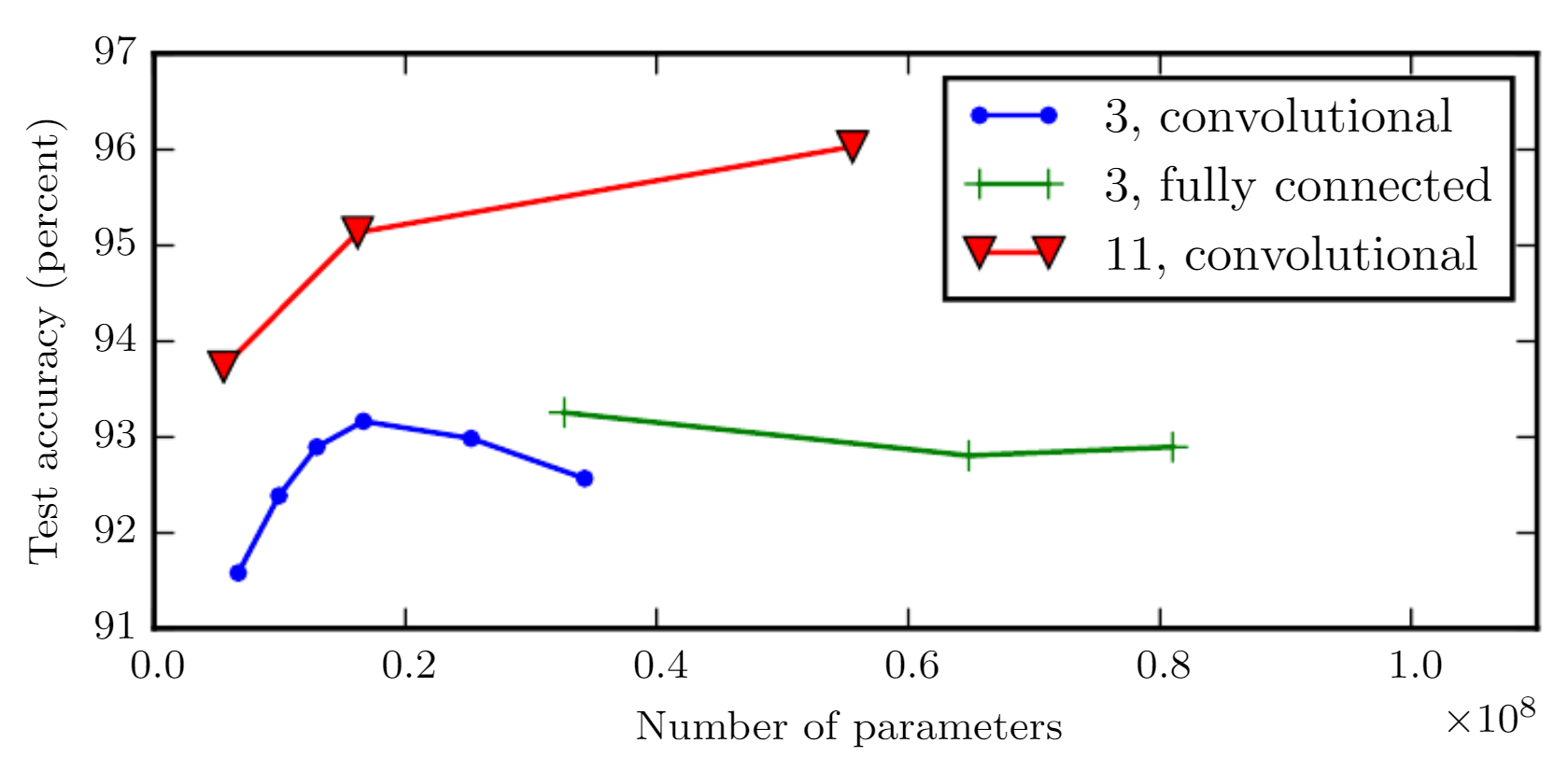
모델의 depth는 고정하고, 파라미터의 개수만 바꾼 결과이다. 3층 convolution과 fully connected의 결과를 보면 파라미터의 개수가 늘어날수록 정확도가 높아지다가 오히려 떨어지는 결과를 확인할 수 있다. 반대로 깊은 11층 convolution의 경우 파라미터의 개수가 늘어날 수록 정확도가 상승하였다. 깊게 모델을 쌓는다는 것은 상대적으로 간단한 함수들로 타겟 함수를 표현하겠다는 의미이고 이는 더 단순한 표현의 학습으로 이어지게 된 결과로 얕게 쌓은 경우보다 과적합을 줄여준다.
Other Architectural Considerations
지금까지는 신경망이 여러 층이 사슬처럼 연결된 단순한 구조에 대해 보았고, 신경망의 depth와 layer의 width에 대해 관심있게 보았다. 하지만 실제 응용에 쓰이는 신경망 구조는 더욱 다양하다.
신경망 구조에서는 특정 Task에 특화된 구조가 많다. 특히 Chapter 9에서 볼 Convolutional Network는 컴퓨터 비전에 특화된 신경망이고, Chapter 10에서 볼 Recurrent Neural Networks는 순차 데이터에 특화된 신경망으로 Feedforward network와는 다른 고려점들이 존재한다.
또한 신경망 층들이 꼭 Chain 형태일 필요는 없다. 물론 chain 형태를 가장 많이 쓰긴 하지만, 여기에 추가적으로 $i$번째 layer에서 $i+1$이나 그 이후의 레이어에 직접 연결에 결과에 더하는 Skip Connection은 출력 layer에서 입력 layer에 가까운 layer들에 gradient 전달을 돕는다.
그 외에도 한 쌍의 layer들 사이의 연결에 대한 고려 등이 있다. 이를 잘 활용한 것이 컴퓨터 비전 분야의 convolution network이다. 이 네트워크는 입력 layer의 각 단위가 출력 layer의 일부 단위들에만 연결이 된다. 이에 대해서는 Chapter 9에서 더욱 자세히 살펴보도록 하자.
Back-Propagation and Other Differentiation Algorithms
Feedforward Network에서는 입력 $x$는 출력 $y$로 나오기 위해 신경망을 따라 앞으로 흘러간다. 앞서 말했듯이 이렇게 정보가 앞으로 흐르는 것을 Feedforward(순전파)라 말하며 결과적으로 하나의 Scala cost $J(\theta)$를 얻는다. 한편 Feedforward의 역방향으로 정보가 흐르는 Back-Prop(역전파) 또한 있는데 이것이 바로 각 지점에서 기울기를 간단하고 빠르게 구할 수 있는 알고리즘이다.
종종 Back-Prop이 Multi layer NN의 학습 알고리즘 그 자체라고 생각하는 오해가 있다. 하지만 Back-Prop은 단순히 기울기를 계산하는 알고리즘이지 학습을 하기 위해서는 SGD와 같은 다른 알고리즘이 필요하다. 또한 Back-Prop을 Multi Layer NN에서만 사용하는 알고리즘이라는 오해가 있는데 Back-Prop은 모든 미분 가능한 함수의 기울기를 구할 수 있기 때문에 굉장히 Universal한 알고리즘이다.
Computational Graph
계산 그래프란 역전파 알고리즘의 설명을 도와주는 수학적 도구로 본 책에서의 그래프의 각 노드는 하나의 변수를 의미한다. 이때 변수는 스칼라, 벡터, 행렬, 텐서 등이 될 수 있다.
이 계산 그래프에는 Operation이라는 개념을 도입해야 하는데, Operation이란 하나 이상의 변수들을 input으로 받는 함수로, Computational Graph에서는 아래 그림처럼 유향 간선의 끝에 Operation을 표기하기도 한다.

Chain Rule of Calculus
Chain Rule of Calculus(미분의 연쇄 법칙)는 derivatives가 알려진 여러 함수들을 이용해 만든 특정 함수의 derivative를 구하는데 사용하는 기법이다. 예를 들어 $x$가 하나의 실수이며, $f,g$가 실수를 실수로 사상하는 함수, $y=g(x), z = f(y) = f(g(x))$라 하자. 이는 연쇄법칙에 의해 다음이 성립한다.
$$
{dz\over dx} = {dz\over dy} {dy\over dx}
$$
이를 벡터로 확장해보자. $x\in \mathbb R^m, y\in \mathbb R^n$이며, $g: \mathbb R^m \rightarrow \mathbb R^n, f: \mathbb R^n \rightarrow \mathbb R$인 경우 다음이 성립한다.
$$
{\partial z\over \partial x_i} = \sum_j{\partial z\over \partial y_j}{\partial y_j\over \partial x_i}\
\nabla_xz = ({\partial y\over \partial x})^\top \nabla_yz \text{ (vector notation)}
$$
이때 $\partial y \over \partial x$는 $g$의 $n\times m$ Jacobian matrix이다. 즉, 변수 $x$의 기울기는 Jacobian matrix $\partial y \over \partial x$에 기울기 벡터 $\nabla_yz$를 곱하여 구할 수 있다. (이후 텐서의 Chain Rule 설명은 생략)
Recursively Applying the Chain Rule to Obtain Backprop
먼저 Notation에 대해 정의하고 Feedforward 알고리즘에 대해 보도록 하자.
- $u^{(n)}:$ input의 cost 값
- $u^{(i)}:$ $u^{(n)}$의 ancient 노드
- $\mathbb A^{(i)}:$ $u^{(i)}$의 parent 노드의 집합
- $f:u^{(i)} = f^{(i)}(\mathbb A^{(i)})$와 같이 parent 노드들로 $u^{(i)}$를 매핑하는 함수 $f$

단순히 이번에 구해야하는 값 $u^{(i)}$를 구하기 위해 그냥 $u^{(i)}$의 parent 노드들의 집합 $\mathbb A^{(i)}$를 만들고 이 집합에 함수 $f$를 적용해 $u^{(i)}$를 반복적으로 구하는 알고리즘이다.
이때 Chain Rule에 의해 $u^{(j)}$에 대한 $u^{(n)}$의 변화량(기울기)은 다음과 같이 정의된다.
$$
{\partial u^{(n)}\over \partial u^{(j)}} = \sum_{i:j\in pa(u^{(i)})}{\partial u^{(n)}\over \partial u^{(i)}}{\partial u^{(i)}\over \partial u^{(j)}}
$$
즉, $u^{(j)}$에 대한 $u^{(n)}$의 변화량(기울기)은 $u^{(j)}$의 자식 노드들의 기울기$\times u^{(j)}$에 대한 자식 노드들의 변화량으로 정의된다.
Duplicated Computing in Back-Prop
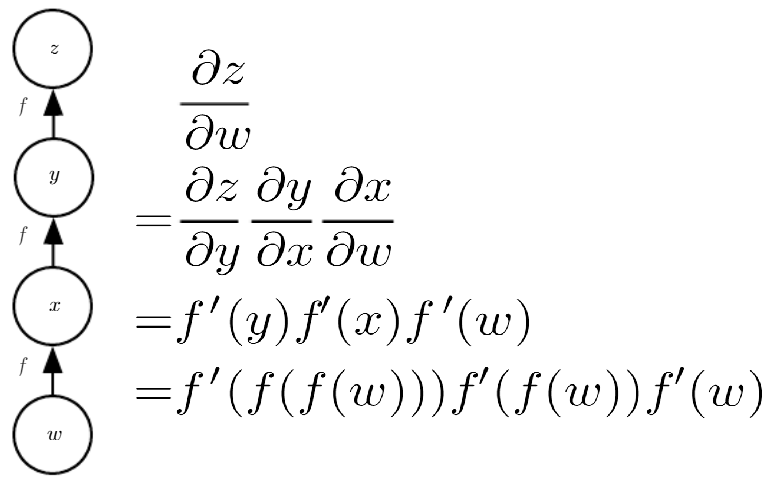
위의 예시처럼 Back-Prop시 같은 함수를 여러번 계산해야 하는 경우가 발생할 수 있다. 이런 경우 $f(w)$의 값을 한 번만 계산하여 변수 $x$에 저장해 두면 계산 비용을 감소 시킬 수 있다. 하지만 메모리가 제한적인 경우 그냥 식의 마지막 부분처럼 매번 모든 계산을 하는 방식도 유효한 방식이 될 수 있다. 이 방식으로 구현한 알고리즘이 아래와 같다.

grad_table 에 각 노드의 기울기를 저장하며, 이전에 계산해 둔 ${\partial u^{(n)} \over \partial u^{(i)}}$와 ${\partial u^{(i)} \over \partial u^{(j)}}$를 곱해 ${\partial u^{(n)} \over \partial u^{(j)}}$를 구하는 방식이다. 이 알고리즘의 계산 복잡도는 계산 그래프 $\mathcal G$의 edge 개수에 비례한다. (각 노드당 1회의 Jacobian Matrix를 구하는 연산과 동일하다.)
이 방식과 달리 계산 그래프를 단순화해서 subexpression을 피하는 방식이나 매번 계산해 메모리를 절약하는 방식 또한 있을 수 있다.
Symbol-to-Symbol Derivatives
계산 그래프는 특정 값이 없는 Symbol에서 작동하며 이러한 표현을 Symbolic representation이라 부른다. 실제 신경망에서는 이러한 Symbol을 수치로 대체하여 계산하게 된다.
Back-Prop 방식은 크게 Symbol-to-Number 방식과 Symbol-to-Symbol 방식이 있다.
- Symbol-to-Number: 계산 그래프와 그 입력으로 쓰이는 수치를 받고 그 입력에 대한 기울기를 리턴한다. 이러한 방식은 Caffe, Torch 등의 라이브러리에서 사용한다.
- Symbol-to-Symbol: 계산 그래프를 받고 도함수들의 Symbol representation을 제공하는 노드를 그래프에 추가하는 방식으로 Back-Prop 진행. Theano, TensorFlow등의 라이브러리에서 사용한다.
본 교재는 Symbol-to-Symbol 방식에 대해서 주로 다룬다.
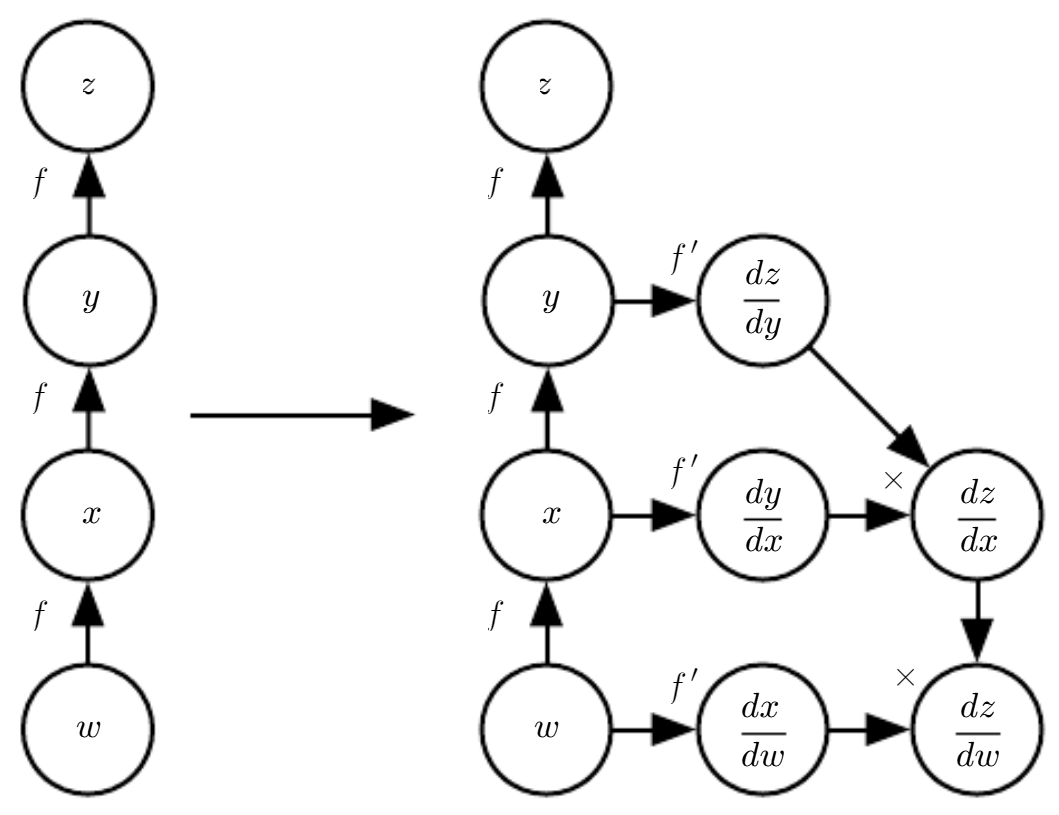
Symbol-to-Symbol의 경우 Back-Prop 알고리즘은 위 그림처럼 구체적 실 수치에 접근할 필요 없이 도함수를 계산하는 방법에 대한 노드를 그래프에 추가한다.
기존 노드들과 같은 data structure의 도함수 계산 노드를 추가해 주기만 하면 되기 때문에 기존 언어로 도함수를 representation 가능하다는 장점이 있으며, 이는 사실상 Symbol to Number 방식을 포함한다. Symbol to Number와의 차이는 명시적 Graph를 산출하는가 아닌가이다.
General Back-Propagation

- get_operation(V): V를 계산하기 위한 연산들을 리턴
- get_consumers(V, G): 계산 그래프 G에서 V의 자식 노드들의 집합을 리턴
- get_inputs(V, G): 계산 그래프 G에서 V의 부모 노드들의 집합을 리턴
- op.bprop($inputs$, $\bold x$, $G$): $\sum_i(\nabla\bold x op.f(inputs)_i)G_i$를 리턴
- $inputs:$ operation을 위한 입력
- $\bold x:$ 기울기를 계산하고자 하는 입력
- $G:$ 연산 출력에서의 기울기
- $op.f:$ 실제 operation의 수학 함수
각 연산의 평가 비용이 같다 가정 시 노드가 $n$개인 그래프의 기울기를 계산하는 비용은 $O(N^2)$을 넘지 않으며, 이때 출력을 저장해야 할 연산의 수도 $O(N^2)$을 넘지 않음. 즉, Generalized Back-Prop의 시간 복잡도와 공간 복잡도는 둘 다 $O(N^2)$이라는 의미이다. 이때 말하는 연산은 계산 그래프의 최소 구성 단위를 말한다. 즉, 여러 번의 곱셈과 덧셈이 필요한 행렬 연산 또한 한번의 연산으로 간주한다.) 실제 흔히 쓰이는 계산 그래프의 경우는 이보다 훨씬 적어진다. 실제 흔히 쓰이는 계산 그래프들은 거의 Chain 구조로 cost function들이 연결되어있어 Back-Prop의 비용이 $O(n)$이다.

이전에 본 재귀 형태의 기울기 계산을 재귀가 아닌 형태로 바꾸어 나타내어보면 노드 $j$에서 노드 $n$으로의 경로가 지수적으로 증가하게 되어 계산량이 매우 많아진다. 동일한 $\partial u^{(i)}\over \partial u^{(j)}$의 계산을 피하기 위해 일반적인 Back-Prop은 중간 결과 $\partial u^{(n)}\over \partial u^{(i)}$를 저장해두며 이를 계산할 필요가 발생한다면 저장해둔 결과를 사용한다. 이는 Dynamic Programming으로 많이 알려진 알고리즘이다.
Complications
위의 Back-Propagation 알고리즘은 실제 구현들보다 단순화된 형태로 실제 구현상에서는 여러 텐서를 돌려주거나 부동 소수점 등에 대한 처리도 세심하게 설계해야 할 필요가 있으며, 기울기가 정의되지 않는 경우 등 여러 예외에 대한 처리를 해주어야 한다.
또한 각 텐서를 계산하는 즉시 버퍼에 텐서를 더하는 방식을 활용해 메모리 소비량을 제어하는 방식 또한 고려해야 한다.
그 외에도 실제 구현 시 복잡해지는 여러 기술적 어려움이 존재한다. 이를 극복하기 불가능할 정도로 어렵지는 않으나 이렇게 위에서 언급하지 않은 까다로운 사항들이 실제 구현에는 많이 있다는 점을 꼭 감안해야 한다.
Differentiation outside the Deep Learning Community
Deeplearning 커뮤니티는 컴퓨터 과학 커뮤니티와 분리되어 성장해왔다. 그 과정에서 Deeplearning의 미분을 수행하는 과정은 자신만의 문화적 태도를 형성했다. Back-Prop은 자동 미분이라는 알고리즘적으로 미분을 구하는 분야의 한 갈래이며, Back-Prop은 자동 미분의 일종인 reverse mode accumulation의 special case이다.
그렇기에 Back-Prop과는 다른 방식으로 기울기를 계산하는 방식들이 존재한다. 일반적으로 최적의 연산 순서를 구하는 문제는 각 대수식을 가장 비용이 낮은 형식으로 단순화 하는 과정들이 요구되며 이는 NP-완전 문제에 해당된다. 그렇기에 최적의 연산 순서를 구하는 것은 매우 어려운 문제이다. 그렇기에 Back-Prop이 최적의 연산 순서가 아니고, foward mode accumulation이라는 기울기를 앞에서부터 계산하는 방식이 더 효율적인 경우가 존재한다. 예를 들어 $ABCD$라는 식에서 $A$의 행이 $D$의 열보다 적다면, 이 경우 forward mode accumulation이 Back-Prop보다 효율적이다.
정리하자면, Back-Propagation은 현재 가장 많이 사용되는 기울기 계산 알고리즘이지만, 유일한, 최적의 기울기 계산 방식이 아니다.
Higher-Order Derivatives
Higher Order Derivatives(ex. 이계도함수)는 Theano, TensorFlow와 같은 Symbol to Symbol 방식의 라이브러리에 기존 Graph를 서술하는 방식으로 똑같이 서술 가능함
이계도함수를 계산 하는 경우는 대부분 Hessian Matrix과 관련 있으며 Hessian Matrix는 $N\times N$ 행렬인데 보통 Deepleanring에서 $N$은 수 십억 이상인 경우가 종종 발생한다. 이러한 경우 Hessian Matrix를 직접 구할 수 없기 때문에 Krylov Method라는 방식을 이용해 Hessian Matrix를 근사하게 된다. 이 방식은 행렬의 역행렬이나 고유 벡터, 고유 값등을 행렬 - 벡터 곱 만을 이용해 근사하는 반복적 기법들을 일컫는 용어이다.
$$
Hv = \nabla_x[(\nabla_xf(x))^\top v]\
H:\text{Hessian Matrix}
$$
이렇게 Hessian Matrix를 계산 가능하지만, 대체로 Hessian Matrix의 계산은 피하는 것을 권장한다.
'공부 및 정리 > DeepLearning Book' 카테고리의 다른 글
| 9. Convolutional Neural Networks (0) | 2022.12.20 |
|---|---|
| 7. Regularization for Deep Learning (0) | 2022.12.20 |
| 5. Machine Learning Basics (0) | 2022.10.10 |
| 4. Numerical Computation (0) | 2022.10.10 |
| 3. Probability Theory (0) | 2022.10.10 |
