머신러닝 알고리즘들은 많은 수치적 계산을 필요로 하는데, 머신러닝 알고리즘들은 보통 공식을 풀어내는 것이 아닌 반복 프로세스를 통해 추정치를 업데이트하는 방식으로 해결하기 때문이다.
이때 디지털 컴퓨터에서는 무한히 많은 실수를 한정된 메모리로 표현하려다 보니 정확하게 표현하는 것이 어려워 여러 수치적 문제가 발생할 수 있음
Overflow and Underflow
유한한 Bit 수로 무한히 많은 실수를 표현하려다 보니 approximation 에러가 발생한다. 이는 대부분 Rounding error라 불리는 반올림 오류로 매우 사소해 보이지만 이를 처리해주지 않는다면, 이론에서는 가능했던 것이 실제에서는 에러가 발생하는 경우가 있다.
이러한 Rounding Error의 좋은 예시로 Underflow가 있다. Underflow는 0 근처의 수가 0이 되어버리는 오류로 이로 인해서 여러 오류가 발생하는데, 예를 들어 division by zero나 0의 log와 같은 오류를 발생 시킬 수 있다.
또 다른 중요한 수치 오류로는 Overflow가 있다. Overflow는 수가 $\infty$이나 $-\infty$과 같이 수치상 매우 커질 때 발생하게 된다.
이러한 Overflow나 Underflow를 주의해야 하는 함수로는 Softmax function이 있다. Softmax는 보통 multinoulli distribution과 관련된 확률을 예측 시 사용하게 되는데, 다음과 같은 수식으로 정의된다.
$$
softmax(x)_i = {exp(x_i) \over \sum^n_{j=1} exp(x_j)}
$$
위 식은 특정 값이 전체 값에서 차지하는 비율을 나타내어주는 함수로 볼 수 있으며, 만약 위 함수에서 모든 값이 상수 $c$로 동일한 경우 모든 값의 softmax 값은 $1\over n$으로 동일하다.
이때 만약 $c$가 매우 작은 음수라 생각해 보자. $exp(c) \approx 0$ → $\sum^n_{j=1}exp(c) \approx 0$
즉, Underflow가 발생하여 위 식의 분모 부분이 0이 되어 정의가 되지 않는다는 문제가 발생한다.
반대로 $c$가 매우 큰 양수라 생각해보자. $exp(c)$는 Overflow가 발생하여 이 또한 정의가 되지 않는다.
이러한 문제는 $\text{softmax}(z), z=x-\max_i(x_i)$로 해결 가능하다.
만약 가장 큰 $x$의 경우 $\max_i(x_i)$로 빼주게 되므로, 0이 되어 overflow를 방지하며, 만약 가장 작은 $x$의 경우 그냥 최댓값으로 빼주어 분자는 0, 분모는 아무리 작더라도 최소 1은 ($max_i(x_i) - max_i(x_i) = 0 \rightarrow exp(0) = 1$) 남게 되어 underflow를 방지해 overflow와 underflow 둘 다 해결 가능하다.
하지만 이는 일반 softmax의 해결책이며, logsoftmax의 경우 $x$값이 매우 작은 경우 softmax의 값이 0이 되어 log를 취할 수 없게 된다. 이 경우 또한 위에서 한 트릭을 똑같이 이용해주면 해결 가능하다.
$$
\begin{align}
\text{log softmax}(x) &= \log({\exp(x)\over \sum_iexp(x_i)}) \\
&= \log({\exp(x-max_i(x_i))exp(max_i(x_i))\over \sum_iexp(x_i-\max_i(x_i))exp(\max_i(x_i))}) \\
&= (x-\max_i(x_i)) - \log(\sum_iexp(x_i-\max_i(x_i)))
\end{align}
$$
하지만 tensorflow나 pytorch와 같은 좋은 라이브러리를 이용하면 이러한 수치적 문제를 대부분 해결 가능하다.
Poor Conditioning
Conditioning이란 함수의 input에 대한 민감도를 나타낸다. 이때 민감도가 높다면, input이 조금만 바뀌어도 결과 값에 큰 차이를 준다는 의미이다. 이렇게 입력에 대한 민감도가 높다면, 위에서 알아본 rounding error의 영향을 매우 크게 받아 결과에 대한 큰 오류를 발생시킬 수 있다.
$$
A\textbf x = \textbf b
$$
위 식에서 행렬 $A$의 민감도가 높은 경우 입력 $textbf x$의 미세한 값 차이에도 $textbf b$의 값이 크게 바뀔 수 있다는 것이다.
$f(x) = A^{-1}x$에서 $A\in \mathbb R^{n\times n}$이고, 고유값 분해가 가능하다 할 때 condition number는 다음과 같다.
$$
\max_{i,j}|{\lambda_i \over \lambda_j}|
$$
위 식은 고유값 분해 후 (가장 큰 eigenvalue / 가장 작은 eigenvalue의 절댓값)이 될 것이다. 이 condition number가 커지면, 역행렬은 입력의 오차에 민감해진다.
이러한 민감도는 행렬 자체의 특성이지 역행렬을 구하는 동안의 rounding error의 결과가 아니다.
즉, 민감도가 큰 행렬에서 미세한 입력의 변화를 rounding error 때문에 감지해내지 못한다면 결과에 큰 영향을 끼쳐 시스템이 굉장히 불안정해진다는 것이다.
이러한 불안정성이 일어나는 이유에 대해서는 책에서 설명을 해주지 않았는데, 아마도 행렬 $A$의 선형 종속인 열들 때문일 것이다. 위 수식에서도 보이듯이 위 수식이 커지기 위해서는 가장 큰 eigen value $\lambda_i$가 커지거나, 가장 작은 eigen value $\lambda_j$가 0에 가까워지거나 둘 중 하나이다.
이때 eigen value는 특정 기저로 커지는 크기를 나타내는 값으로 열벡터들이 선형 종속인 경우 이 값은 0이 나올 수 있다. 이때 열 벡터들이 서로 독립이지만 거의 선형 종속인 열 벡터가 존재한다면, 그 벡터만이 가리키는 방향의 크기는 매우 작으므로 고유값 분해시 eigen value가 매우 작은 값이 존재하게 되어 결국 condition number는 매우 커지게 될 것이다.
Gradient-Based Optimization
대부분의 머신러닝 알고리즘들은 optimization 과정을 수반한다. Optimization이란 어떤 함수 $f(x)$에서 $x$를 수정해 가며 함수값을 최소-최대화 하는 과정을 의미한다. 보통 Optimization란 최소화 하는 과정을 의미하는데, $f(x)$를 최소화 하는 것은 $-f(x)$를 최대화 하는 것과 같으므로 크게 중요하지는 않다.
위에서 언급한 최대-최소화 하고 싶은 함수 $f(x)$를 objective function, 또는 criterion이라 부르며, 이 함수를 최소화 할 때 cost function, loss function, error function이라 부르며, 최소-최대로 만들어 주는 point $x$는 * 첨자를 붙여 $x^\ast = \text{argmax} f(x)$가 된다.
최적화를 본격적으로 알아보기 전 간단한 미적분 지식을 되새기고 가자. 어떤 함수 $y = f(x)$가 있을 때 이 함수의 derivative는 $f'(x)$ 또는 $dy\over dx$로 표기한다. $f'(x)$는 $f(x)$의 점 $x$에서의 기울기를 나타내며, 점 $x$에서 미소 변화 $\epsilon$이 발생시 이 점에서의 기울기 만큼 선형적으로 변화해 $f(x + \epsilon) = f(x) + \epsilon f'(x)$이 된다는 의미이다.
이처럼 $x$를 어떻게 움직여야 함수의 값이 작아지는지에 대해 알려주는 덕에 미분은 함수의 최소화에 매우 유용하다. 즉, 기울기를 따라 움직이면, 커지므로, 기울기의 반대로 조금씩 움직여 가며 $f(x)$의 값을 줄여갈 수 있고 이러한 기법을 gradient descent라 부른다.

위 그림은 앞서 설명한, gradient descent의 간단한 시각적 설명을 돕는다.
$f'(x) = 0$인 경우 미분은 더 이상 움직임의 방향에 대한 정보를 주지 못한다. 이러한 미분이 0인 점을 critical points 또는 stationary points라 부른다.

Local minimum은 모든 주변 이웃 점들보다 작은 점을 의미하며, 그러므로 더 이상 줄어들 가능성이 없는 점이다. 반대로 Local maximum은 모든 이웃점들보다 큰 값을 가진 점을 의미한다. 그러므로 이 점에서는 더 이상 늘어날 가능성이 없는 점이다. 마지막 critical point로는 앞서 말한 maxima 또는 minima 둘 다 아닌 점이 있다. 이러한 점을 saddle point라 말한다.
global minimum은 함수의 전체 치역 중 가장 작은 value를 의미한다. 이러한 global minimum은 여러 개가 존재할 수도 있고, local minimum은 global minimum이 아닐 수 있다.

딥러닝에서 objective function은 고차원적이기 때문에 최적이 아닌 local minimum과 평평한 지역의 saddle point가 매우 많아 최적화 하기 매우 어렵다. 그렇기 때문에 보통 global minimum이 아닌 그냥 local minimum 중 매우 낮은 곳을 채택한다.
위 그림을 참고해보면, 꼭 global minimum이 아닌 첫 번째 local minimum도 상당히 낮기 때문에 local minimum을 채택한다. 하지만 두번쨰 local minimum은 다른 더 낮은 곳이 많기에 이곳은 채택하지 않는다.
보통 우리가 최소화 하고 싶은 경우들은 다중 입력에서 스칼라 출력을 얻는다. $(\mathbb R^n\rightarrow \mathbb R)$ 이렇게 다중 input을 가진 함수들에 대해서는 partial derivatives (편미분)의 개념을 사용해야만 한다.
partial derivatives는 $\frac{\partial}{\partial{x_i}} f(x)$로 표기하고 이는 $x_i$ 하나의 변수가 증가할 때 $f$의 변화를 나타낸다.
gradient는 벡터 관점의 derivative의 일반화된 개념으로 $f$의 gradient는 모든 partial derivatives를 포함하는 벡터로 $\nabla_xf(x)$로 표기한다. gradient의 i번째 요소는 $x_i$ 관점의 $f$의 partial derivative이며, 위에서 보았던 critical point들에서의 gradient의 모든 요소는 0이다.
방향 $u$의 directional derivative(방향 도함수)는 함수 $f$의 방향 $u$로의 경사를 의미하며, 이를 이용해 가장 빠르게 $f$를 최소화 하는 방향을 찾을 수 있다.
$$
\min_{u,u^\top u = 1} u^\top \nabla_x f(x) = \min_{u, u^\top u = 1} ||u||_2 ||\nabla_x f(x)||_2 \cos \theta
$$
$$
\theta:\text{angle between }u\text{ and gradient}
$$
이때 $u$와 관련 없는 $||\nabla_xf(x)||$를 제외하고, $||u|| = 1$이라 하면, 결국 $\cos\theta$를 최소화 하는 것이 되고 이는 $\theta$를 최대화 하는 것이다. ($\theta = \pi$) 이는 결국 gradient의 반대 방향을 의미하게 되며, gradient대로 움직이면 함수를 따라 올라가게 되는 것을 의미하므로 즉, 함수를 최소화 하기 위해서는 negative gradient로 움직여야 한다. 이러한 기법을 gradient descent 또는 steepest descent 방법론이라 알려져 있다.
$$
x' = x - \epsilon \nabla_xf(x)
$$
gradient descent는 위와 같은 공식으로 새로운 점으로 이동하게 된다. 이때 $\epsilon$은 learning rate로 작은 양의 scalar 값이다. 이 learning rate는 일반적으로 작은 양의 상수로 설정한다. 그 외에도 여러 $\epsilon$ 값에 대해 $f(x-\epsilon\nabla_xf(x))$의 값을 평가하고 가장 objective 함수의 값이 작은 결과를 선택하는 line search 방식이 있다.
gradient descent는 gradient의 모든 element가 0일때. 즉, 모든 방향으로의 도함수가 0일때 수렴한다.
Beyond the Gradient: Jacobian and Hessian Matrices
입력과 출력 모두가 벡터인 함수의 모든 partial derivatives를 포함한 것이 Jacobian Matrix $J$이다.
$$
\begin{matrix}
f:\mathbb R^m \rightarrow \mathbb R^n. \rightarrow J \in \mathbb R^{n\times m}\\
J_{i,j}={\partial\over\partial x_j}f(x)_i
\end{matrix}
$$

이때 $f_1, f_2, ..., f_m$은 함수 $f$의 m개의 출력 구성 요소이며, $x_1, x_2, ..., x_n$은 n개의 입력 변수이다. 즉, 입출력이 벡터인 함수에서 모든 입력 요소들로 모든 출력 요소들을 미분한 것을 행렬로 만든 것이 Jacobian Matrix $J$이다.
이 Jacobian Matrix는 이 책에서는 Deep Learning의 기초를 다루기에 딱히 깊게 다루지 않으며 실제로 기본적인 딥러닝 학습에서도 방금 본 Gradient나 앞으로 볼 Hessian Matrix를 더 자주 사용한다.
암튼 이제 도함수의 도함수. 즉, second derivative(이계도함수)에 대해 생각해보자. 이계도함수는 도함수의 변화에 대해 나타내며, 이는 curvature(곡률)을 측정한다.

위 그림을 보면 이계도함수의 부호에 따라 여러 특성이 있다. (점에서의 기울기는 1이라 가정한다.)
- 이계도함수가 음수인 경우 함수는 위로 볼록하며, $\epsilon$ 만큼 gradient descent한 경우 $\epsilon$보다 많이 감소한다.
- 이계도함수가 0인 경우 그 점의 곡률은 없는 flat line을 의미한다. 즉, $\epsilon$만큼 gradient descent한 경우 $\epsilon$ 만큼 감소한다.
- 이계도함수가 양수인 경우 함수는 아래로 볼록하며, $\epsilon$ 만큼 gradient descent한 경우 $\epsilon$보다 적게 감소한다.
$f: \mathbb R^n \rightarrow \mathbb R$ 스칼라 함수의 두번째 편미분들의 행렬로 Hassian Matrix $H(x)$라 부르며, 이는 Gradient의 Jacobian이라 볼 수 있다.
$$
H(f)(x)_{i,j} = {\partial^2 \over \partial x_i \partial x_j}f(x)
$$

이때 중요한 특성으로 commutative(교환법칙)이 있다. 간단히 표현해 $H_{i,j} = H_{j,i}$라는 점으로 이는 $H$가 symmetric 행렬이라는 것을 나타낸다.symmetric 행렬은 고유값 분해 측면에서 매우 좋은 특성을 지니는데, 실수의 symmetric 행렬은 언제나 실수의 고유값 및 basis인 orthogonal eigen vector들로 분해가 가능하다는 특성이 있다.
단위 벡터(크기 1) $d$가 있을 때 $d^THd$는 특정 방향 d로의 함수의 이차 미분을 나타내게 된다. 즉, 이 결과는 특정 방향 d로의 함수의 곡률을 나타내게 된다는 것이며, 이 방향이 $H$의 eigen vector인 경우 이 결과 (함수의 곡률, 이계도함수)는 해당 eigen vector에 맞는 고윳값이 된다. (Hessian Matrix가 Symmetric Matrix이므로 eigen vector들은 서로 수직하여 내적 시 0이 되므로 $d^THd = d^TQ\Lambda Q^T d$는 고윳값만 빠져나오게 된다. eigen vector가 아닌 경우 이계도함수는 고윳값의 가중 평균으로 계산.)
이러한 방향을 가진 2차 도함수는 한번의 gradient descent로 어떤 결과를 보여줄지에 대해서 알려준다. 현재 점 $x^{(0)}$ 주위의 함수 $f(x)$를 아래와 같이 second-order Taylor series approximation로 예측할 수 있다.
$$
f(x) \approx f(x^{(0)})+(x-x^{(0)})^Tg+{1\over 2}(x-x^{(0)})^TH(x-x^{(0)})
$$
$$
g: \text{gradient}, H:\text{Hessian at }x^{(0)}
$$
이때 $(x-x^{(0)})^Tg+{1\over 2}(x-x^{(0)})^TH(x-x^{(0)})$는 gradient descent시 함수값의 변화이다.
learning rate $\epsilon$을 사용하면, 새 점 $x$는 $x^{(0)}-\epsilon g$가 된다. 이 값을 넣어 다시 공식을 보면
$$
f(x^{(0)} - \epsilon g) \approx f(x^{(0)}) - \epsilon g^Tg + {1\over 2}\epsilon^2 g^THg
$$
위 식은 3개의 항으로 이루어져 있다.
- $f(x^{(0)})$: 기존 값
- $-\epsilon g^Tg$: 기울기로 인해 향상되는 값
- ${1\over 2}\epsilon^2g^THg$: 곡률을 반영한 조정 값
이때 마지막 항의 값이 너무 크면, gradient descent의 결과는 오히려 커지게 된다. $g^THg$가 양이 아닌 값이 된다면, Tayler series approximation은 값이 감소할 것을 예측하게 된다. 이때 $\epsilon$의 값이 큰 경우 곡률 또는 gradient가 큰 상황에서는 $g^THg$의 값이 발산해버리기 때문에 $\epsilon$ 값은 휴리스틱한 방식으로 정하게 된다.
$g^THg$가 양수인 경우 learning rate($\epsilon$)를 정하기 위해 아래 수식을 사용한다.
$$
\epsilon^*={g^Tg\over g^THg}
$$
이때 최악의 경우는 $g$가 $H$의 eigenvalue $\lambda_{max}$의 eigenvector와 일치하는 경우이다. 이 경우 최적의 learning rate는 $1\over \lambda{max}$가 되어 매우 작은 learning rate를 사용해야 한다. ($g$는 단위 벡터, 앞서 본 것처럼 $g^THg$에서 $g$가 eigen vector인 경우 해당 eigen value가 나옴) 암튼 이렇게 우리가 minimize하는 함수가 2차 함수에 잘 근사된다면 헤시안 행렬을 이용해 학습률을 설정 가능하다.
또한 이계도함수는 critical point가 local minimum인지, local maximum인지, saddle point인지를 판별 가능하다. 이러한 과정을 second derivative test라 부른다.
- $f''(x) > 0 & f'(x) = 0:$ 아래로 볼록 → local minimum
- $f''(x) < 0 & f'(x) = 0:$ 위로 볼록 → local maximum
- $f''(x) = 0 & f'(x) = 0:$ 알 수 없음 (saddle point나 그냥 평평한 지점)
다차원에 대해서 second derivative test는 Hessian matrix의 고유값 분해를 통해 가능하다.
만약 $\nabla_xf(x) = 0$인 상태에서 Hessian이 positive definite(모든 eigenvalue가 양수)면, local minimum이다. 이는 이계 방향도 함수가 어느 방향이든 양수이다. (Hessian 행렬의 eigenvalue가 해당 eigenvector 방향으로의 이계도함수가 됨) 반대로 Hessian이 negative definite (모든 eigenvalue가 음수)면, local maximum이다. (뭐 당연한 얘기다.)
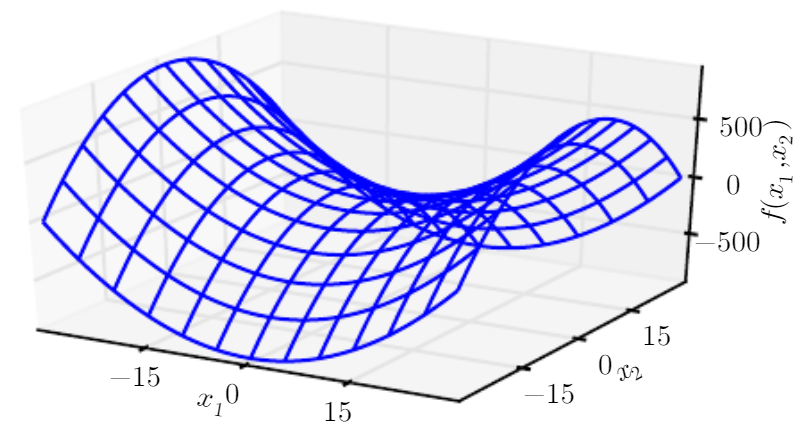
다른 독특한 경우를 보면, 하나 이상의 eigenvalue가 양수이며, 하나 이상의 eigenvalue가 음수인 경우가 있다. 이 경우 한 횡단면으로는 local minimum, 다른 한 횡단면에서는 local maximum이 된다. 위 그림이 이것에 해당되는 경우로 이 경우는 saddle point가 된다.

다변수 함수에서 이계도함수 테스트의 결론을 내릴 수 없는 경우는 1개 이상의 고유값이 0을 가지고, 나머지 고유값이 전부 같은 부호를 가지는 경우이다. 위 그림처럼 죽 직선이 되는 시작점에서 이 지점이 local minimum인지 알 수 없는 것이 이것의 예시이다.
다차원 함수에서는 한 점에서 다양한 방향으로 이계도함수가 있다. 이러한 점에서의 Hessian 행렬의 condition number는 이계도함수가 얼마나 다른지를 측정한다. (condition number의 정의 자체가 $\lambda_{\max}\over \lambda_{\min}$이므로 당연하다.)

이때 Hessian이 poor condition number를 가진다면, 한 방향으로는 빠르게 변하나, 다른 방향으로는 느리게 변하는데, gradient descent는 이러한 변화를 반영하지 못해 성능이 좋지 않고, learning rate를 정하는 것 또한 어렵다. (한 방향으로 너무 빠르게 움직이기 때문에 learning rate를 줄일 수 밖에 없는데, 다른 곡률이 없는 방향으로는 진전이 거의 없기 때문. 좌측 그림 참고)
이러한 문제는 Hessian matrix로부터의 정보를 이용하는 Newton’s method라는 방식으로 해결 가능하다. Newton’s method는 second-order Taylor series expansion을 기반으로 $f(x^{(0)})$ 주변의 값을 근사한다.
$$
f(x) \approx f(x^{(0)})+(x-x^{(0)})^T\nabla xf(x^{(0)})+{1\over 2}(x-x^{(0)})^TH(f)(x^{(0)})(x-x^{(0)})
$$
이 함수를 critical point에 대해 풀면 다음과 같다.
$$
x^\ast = x^{(0)} - H(f)(x^{(0)})^{-1}\nabla_xf(x^{(0)})
$$
만약 $f$가 positive definite 2차 함수인 경우 위 식을 통해 한번에 minimum point를 구해낼 수 있다.
하지만 실제로 2차 함수가 아닌 경우에는 locally positive definite 이차 함수로 근사를 하여 여러번 위 식을 적용해 구해낼 수 있다. 이렇게 반복적으로 근사값을 업데이트하고, 근사값의 minimum으로 점프하는 방식은 경사하강법보다 훨씬 빠르게 critical point에 접근이 가능하다는 장점이 있다.
하지만 이것은 local minimum 근처에서는 좋은 특성이지만, saddle point에서는 오히려 좋지 않은 특성을 가질 수 있다. 8.2.3절에서 알아볼 것이지만, 위 방식은 인근 critical point가 최소일때만 적절하다.
지금까지, 그리고 이 책을 정리하며 앞으로 다룰 대부분의 최적화 알고리즘들은 딥러닝이라는 학문에서 쓰이는 함수들이 매우 복잡한 함수라는 점 때문에 guarantee를 제공하는 경우가 거의 없다. (이때 guarantee란 어떠한 보장을 제공하는 것으로 최적해 찾기, 수렴, 변화율 제한 등 특정 조건이 반드시 일어나는 것을 말한다.)
하지만 딥러닝에서도 guarantee를 얻기 위해 제약을 거는 경우가 존재하는데, Lipschitz continuity(립시츠 연속성)라는 제약이 그 예시이다. Lipschitz continuous 함수 $\mathcal L$는 아래와 같이 정의된다.
$$
\forall x, \forall y, |f(x)-f(y)|\le \mathcal L||x-y||_2
$$
양변을 $||x-y||_2$으로 나누어주면 $|{f(x) - f(y) \over ||x-y||_2}| \le \mathcal L$가 되며 이는 함수 $f$의 변화율이 $\mathcal L$보다 작아야한다는 제약을 거는 것이다. 이 특성은 input에 대한 민감도를 줄여주는 역할을 하게 된다. 이러한 제약은 비교적 약한 제약으로 많은 딥러닝 최적화 문제는 약간의 수정을 통해 Lipschitz continuous 제약을 걸 수 있다. (실제 딥러닝 모델에서는 립시츠 상수 $\mathcal L$을 알아내거나 이를 바탕으로 최적화를 수행하기가 어려워 립시츠 조건을 정확히 충족시키기는 쉽지 않다고 함...)
물론 가장 성공적인 최적화 분야는 Convex optimization (볼록 최적화)이다.
볼록 최적화 알고리즘들은 강력한 제약을 걸어 많은 보장을 받을 수 있으나 이는 볼록 함수에만 적용(모든 곳의 Hessian이 Positive semidefinite (eigenvalue가 음이 아닌 수)) 이 가능하다는 한계점이 있다. (이러한 함수는 saddle point가 없고 local minima가 global minima이기 때문에 최적화가 잘 됨)
그렇기에 볼록 함수를 보장하기 어려운 딥러닝 분야에서는 중요도가 떨어져 대부분 딥러닝 알고리즘의 수렴 증명 같은 서브 루틴으로 사용한다.
Constrained Optimization
전체 $x$에 대해서가 아닌 어떤 subset $\mathcal S$ 에 속하는 $x$의 함수 값 $f(x)$를 최대-최소화 시키려는 것을 Constrained Optimization이라 부른다. (이러한 점 $x$를 feasible point라 부른다.)
제약 최적화에 대한 간단한 접근 방식은 제약 조건을 고려하여 gradient descent를 사용하는 것이다.
$\epsilon$과 같은 작은 step size로 gradient descent 후 제약 조건 $\mathcal S$ 에 project 해주면 된다.
좀 더 복잡한 방식으로는 Constrained Optimization problem으로 변환 가능한 unconstrained optimization problem을 설계하여 해결하는 방식이다.
예를 들어 $x\in \mathbb R^3$, $x$가 unit $\mathcal L^2$ norm을 갖는 제약 조건을 가진 $x$의 $f(x)$를 최소화하는 문제가 있을 때 이 대신 $g(\theta) = f([cos\theta, sin\theta]^T)$ 를 최소화 하는 문제로 풀 수 있다. 결과적으로 $[cos\theta, sin\theta]$가 원래 문제의 solution이 된다.
이러한 방식의 풀이는 창의성과 각 문제 별로 특화된 풀이로 존재하게 되어 일반적이진 못하다.
Karush-Kuhn-Tucker (KKT) 접근법은 constrained Optimization의 매우 일반적인 해결책을 제공한다.
KKT는 generalized Lagrangian을 사용하는데 Lagrangian을 정의하기 위해서는 $\mathcal S$를 등식과 부등식의 관점에서 보아야 한다.
$\mathcal S$를 $m$개의 $g^{(i)}$와 $n$개의 $h^{(j)}$의 관점으로 $\mathcal S={x|\forall i, g^{(i)}(x) = 0 \text{ and }\forall j, h^{(j)}(x)\le 0}$ 와 같이 정의하며, 이때 $g^{(i)}$를 equality constraints, $h^{(j)}$를 inequality constraints라 부른다.
여기서 KKT multiplier(KKT 승수)라 불리는 새 변수 $\lambda_i$와 $\alpha_i$를 추가해 generalized Lagrangian은 다음과 같이 정의된다.
$$
L(x,\lambda, \alpha) = f(x) + \sum_i\lambda_i g^{(i)}(x) + \sum_j\alpha_j h^{(j)}(x)
$$
이 unconstrained optimization을 이용해 constrained minimization 문제를 풀 수 있다.
적어도 하나의 feasible point가 존재하며, f(x)가 $\infty$을 갖지 않는다면, $\min_x \max_\lambda \max_{\alpha, \alpha \ge 0}L(x,\lambda, \alpha)$는 $\min_{x\in\mathcal S}f(x)$와 동일한 optimal 목적 함수와 optimal point set을 갖는다.
이는 아래와 같은 특성을 가진다.
$$
\begin{matrix}
\max_\lambda \max_{\alpha, \alpha \ge 0}L(x,\lambda, \alpha) = f(x) \text{ (constraints are satisfied)}\\
\max_\lambda \max_{\alpha, \alpha \ge 0}L(x,\lambda, \alpha) = \infty\text{ (violated constraints)}
\end{matrix}
$$
이러한 특성은 infeasible point가 최적이 될 수 없음과 feasible points 내의 최적이 변하지 않음을 보장한다.
inequality constraints에 대해 조금 더 자세히 살펴보면, $h^{(i)}(x^\ast) = 0$ 인 경우 제약 조건 $h^{(i)}(x)$가 active 라고 말합니다. 만약 제약 조건이 active가 아닌 경우 해당 제약 조건을 사용하여 찾은 solution은 해당 제약 조건이 제거된 경우 최소한 local solution으로 유지된다.
이는 $\min_x \max_\lambda \max_{\alpha, \alpha \ge 0}L(x,\lambda, \alpha) = f(x) + \sum_i\lambda_i g^{(i)}(x) + \sum_j\alpha_j h^{(j)}(x)$에서 $h^{(j)}(x)$가 inactive인 경우 $\alpha_j$이 0이 되어, 제약 조건이 제거되었을 때 $h^{(j)}(x)$가 어떤 값을 갖든 0으로 만들어 버리기 때문이다.
KKT conditions라 불리는 속성들은 constrained optimization problems의 optimal points의 필요 조건이지만 충분 조건은 아니다. (즉, 이러한 condition을 만족하면 optimal point이지만, 모든 optimal points가 이러한 condition을 갖지는 않는다.)
KKT condition은 다음과 같은 조건을 가진다.
- generalized Lagrangian의 기울기가 0
- $x$와 KKT 승수 모두의 모든 제약이 만족
- inequality constraints는 “complementary slackness”: $\alpha \odot h(x) = 0$.
Example: Linear Least Square
$$
f(x) = {1\over 2}||Ax-b||^2_2
$$
위 식을 최소화하는 $x$를 찾는다 가정하자.
선형 대수 알고리즘으로 위 문제를 효과적으로 풀 수 있지만, gradient 기반 최적화 기법을 사용해 풀어보도록 하자.
먼저 gradient를 얻어야 한다.
$$
\nabla_x(x) = A^T(Ax-b) = A^TAx - A^Tb
$$
이 gradient에 작은 값 $\epsilon$을 곱하여 x에서 빼주어 최적화를 진행한다. (아래 알고리즘을 참조)
작은 양수 step size $\epsilon$과 tolerance $\delta$를 정하고 아래 알고리즘을 수행한다.
while $||A^TAx - A^Tb||_2 > \delta$ do:
$x$ ← $x-\epsilon(A^TAx-A^Tb)$
end while
또 다른 방식으로 이전에 공부한 Newton 방식을 사용해 해결 가능하다.
이 경우 true function이 2차이기에 한번에 global minimum으로 수렴이 가능하다.
이번에는 제약을 추가하는 경우에 대한 최적화를 알아보자.
위의 함수를 최소화하며, $x^Tx \le1$이라는 제약을 추가하기를 원한다 가정 시 Lagrangian을 사용할 수 있다.
$$
L(x, \lambda) = f(x) + \lambda(x^Tx-1)
$$
이제 아래 식을 풀면 된다.
$$
\min_x\max_{\lambda, \lambda\ge0} L(x, \lambda)
$$
Lagrangian을 $x$에 대해 미분하여 $A^TAx-A^Tb+2\lambda x = 0$이라는 방정식을 얻을 수 있다.
이를 x에 대해 정리하면 $x = (A^TA+2\lambda I)^{-1}A^Tb$ 이다.
$$
\frac{\partial}{\partial{x}}L(x, \lambda) = x^Tx-1
$$
제약 조건을 만족하는 $\lambda$를 선택해야 하므로, $\lambda$에 대해 gradient ascent를 수행하여 이 값을 찾을 수 있습니다. ($\lambda$의 도함수가 0이 될 때까지 반복)
만약 $x$의 norm이 1 보다 큰 경우 $\lambda$는 최대화 하는 변수이므로 gradient ascent를 해주면 $\lambda$는 점점 커지게 되고 마찬가지로 lagrangian도 커지게 된다.
이는 원래 목적인 lagrangian을 최소화 하는 측면에서 보면 penalty로 볼 수 있으므로 $x$의 norm값은 점차 작아지게 된다. 이를 $x$의 norm이 1에 가까워질 때까지 ($\lambda$의 도함수가 0이 될 때까지) 반복한다.
참고 자료
'공부 및 정리 > DeepLearning Book' 카테고리의 다른 글
| 9. Convolutional Neural Networks (0) | 2022.12.20 |
|---|---|
| 7. Regularization for Deep Learning (0) | 2022.12.20 |
| 6. Deep Feedforward Network (0) | 2022.10.10 |
| 5. Machine Learning Basics (0) | 2022.10.10 |
| 3. Probability Theory (0) | 2022.10.10 |
