SVD를 배웠으니 SVD를 이용한 의사역행렬(Pseudo Inverse)에 대해서 알아보도록 하자.
의사역행렬이란?
의사역행렬이란 Doctor 의사가 아니라 의사 코드(Pseudo Code) 할 때 의사. 즉 가짜 역행렬이라는 것이다.
우리가 이전에 역행렬에 대해서 배웠을 때, 역행렬은 정 사각(Square) 행렬에서만 정의된다고 했었다. 하지만 $m \times n$ 행렬과 같이 정사각 행렬이 아닌 행렬에 대해서도 역행렬과 유사한 역할을 행렬이 있으면 일반적인 상황에서 매우 큰 도움이 될 것이다.
이러한 상황에서 진짜 역행렬은 아니지만 역행렬의 역할을 비슷하게 해주는 행렬을 의사역행렬이라 부른다.
의사역행렬
$$
A = U\Sigma V^T
$$
이전에 특이값 분해에서 우리는 $m \times n$ 행렬 $A$를 위와 같이 분해하였다. 위와 같은 행렬 $A$의 의사역행렬은 아래와 같이 $+$를 첨자로 붙여서 표기하며 분해식도 아래와 같이 표기한다.
$$
A^+ = V\Sigma^+U^T
$$
이때 $\Sigma^+$는 $\Sigma$의 Transpose에 대각 요소들의 값을 역수를 취한 행렬이다. 위와 같이 $A$의 의사역행렬을 정의한 후 $A$와 곱셈시 다음과 같이 된다.
$$
A^+A = V\Sigma^+U^TU\Sigma V^T = V\Sigma^+ \Sigma V^T = I
$$
이때 $\Sigma^+$는 $\Sigma$의 Transpose를 취한 후 대각 요소들의 역수를 취한 행렬이므로 $\Sigma^+\Sigma$는 $n \times m, m \times n$이므로 결과적으로 $n\times n$ 행렬이 되며, 각 요소들은 1이 되고 $VV^T = I$가 되며 이때 결과는 $n \times n$ 행렬이 된다.
이때 위와 같이 의사 역행렬 $A^+$를 좌측에 곱해주는 경우는 $A$가 Full Column Rank인 경우에 결과가 $I$가 나오며 Full Row Rank인 경우 의사역행렬 $A^+$를 우측에서 곱해주어야 $I$가 나오며 이때 결과는 $m \times m$의 행렬이 된다.
Least Squares와 의사역행렬
의사역행렬을 사용하면 Least Squares를 쉽게 풀 수 있었다.
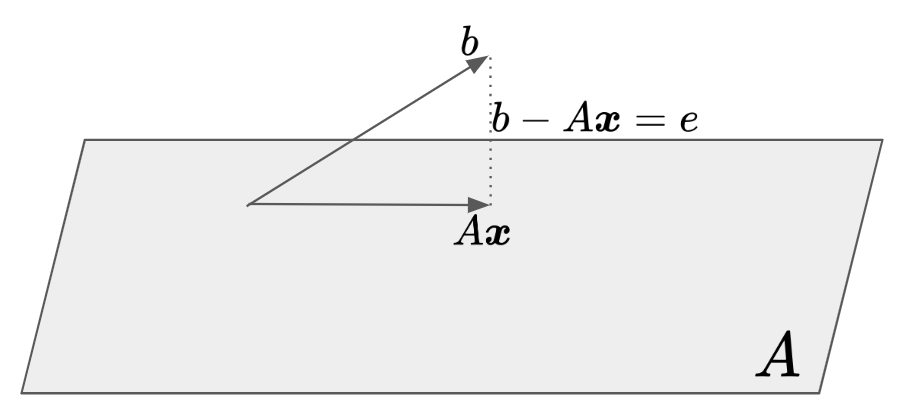
위와 같이 행렬 $A$와 벡터 $b$가 있을 때 $b-A\hat x$와 $A\hat x$는 수직한다라는 속성을 이용해 아래와 같이 풀었다.
$$
\begin{matrix}
\hat x^TA^T(b - A\hat x) = 0 \\
\hat x = (A^TA)^{-1}A^Tb
\end{matrix}
$$
원래 우리가 구하고 싶은 것은 $b\approx A\hat x$를 만족하는 $\hat x$를 찾는 것인데 양 변에 그냥 $A^+$를 곱해주면 그게 $\hat x$이다.
$$
\begin{matrix}
b\approx A\hat x \\
A^+b = \hat x
\end{matrix}
$$
이것이 실제로 맞는지 이전에 얻은 식 $\hat x = (A^TA)^{-1}A^Tb$에 대입해 구해보자.
$$
\begin{align}
\hat x &= (A^TA)^{-1}A^Tb\\
&= (V\Sigma^TU^TU\Sigma V^T)^{-1} V\Sigma^TU^T b\\
&=(V\begin{bmatrix}
\frac{1}{\sigma^2} & \\
& \ddots
\end{bmatrix} V^T) V \Sigma^T U^Tb\\
&= V\begin{bmatrix}
\frac{1}{\sigma} & \\
& \ddots
\end{bmatrix} U^T b\\
&=A^+ b ,(\because A^+ = V\Sigma^+U^T)
\end{align}
$$
즉, $A^+ = (A^TA)^{-1}A^T$라는 것을 알 수 있다. 이것을 Left Pseudo Inverse라 부른다.
물론 Right Pseudo Inverse도 있다. 정리하면 다음과 같다.
- Left Pseudo Inverse : $A^+ = (A^TA)^{-1}A^T$
- Right Pseudo Inverse : $A^+ = A^T(AA^T)^{-1}$
Rank Deficient의 의사역행렬
위에서는 Full Rank의 의사역행렬만을 보았다. 그렇다면 Rank Deficient는 의미 없는 것일까?
Column Rank가 2인 $3\times4$ 행렬 $A$가 있다고 하자. 이 A의 SVD와 의사역행렬은 다음과 같다.
$$
A = U\begin{bmatrix}
\sigma_1 & 0 & 0 & 0 \\
0 & \sigma_2 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{bmatrix} V^T,
A^+ = V\begin{bmatrix}
\frac{1}{\sigma_1} & 0 & 0 \\
0 & \frac{1}{\sigma_2} & 0 \\
0 & 0 & 0 \\
0 & 0 & 0 \\
\end{bmatrix} U^T
$$
이러한 경우의 $AA^+, A^+A$의 결과를 살펴보자.
$$
\begin{align}
AA^+ = U\Sigma^+\Sigma U^T &= U\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{bmatrix}U^T \\
&= u_1u_1^T + u_2u_2^T \\
&\approx u_1u_1^T + u_2u_2^T + u_3u_3^T = I
\end{align}
$$
$$
\begin{align}
A^+A = V\Sigma^+\Sigma V^T &= V\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
\end{bmatrix}V^T \\
&= v_1v_1^T + v_2v_2^T \\
&\approx v_1v_1^T + v_2v_2^T + v_3v_3^T + v_4v_4^T = I
\end{align}
$$
뭐 비슷하게 나올 것이라는 것을 유추할 수 있다. 하지만 상대적으로 $A^+A$는 $AA^+$에 비해 항이 하나 더 누락되었으므로 덜 $I$와 비슷할 것이라는 것을 알 수 있다.
Reference
'공부 및 정리 > 선형대수학' 카테고리의 다른 글
| 행렬의 여러가지 분해 (1) | 2023.10.29 |
|---|---|
| 그람-슈미트 직교화 (Gram-Schmidt Orthogonalization) (0) | 2023.10.29 |
| 특이값 분해 (Singular Value Decomposition) (1) | 2023.10.14 |
| 고윳값 분해 (1) | 2023.10.02 |
| 최소 자승법 (0) | 2023.10.02 |



